Any-order puzzle deduction
I recently wrote here about a complication in puzzle-solving where, in using deductive rules based on the assumption that the puzzle has a unique solution, the ordering of the rules could make a difference in how far you get in the solution. And avoiding this ordering issue by keeping track of more information than just the state of the partially solved puzzle leads to its own difficulties. It seemed like keeping this information could lose you in a maze of undecidable modal logic. For instance in the map coloring puzzle described in that post, we might record information about a partial solution like “I don’t know that this cell is forced to be red, but it is necessary for it to be red in order to prevent a non-unique solution”, with the complexity of these statements growing as the solution progressed. Instead, what I wanted was a way to make decisions without worrying about the order of deduction while only remembering a finite amount of state for each puzzle cell. In the ensuing discussion, @axiom suggested that the extra information should be the order of deductions. That’s not a constant amount of information per cell, but as we’ll see below it works to simplify this even more and remember only which cells were the initial givens and which were deduced later.
To clarify the intuition that deduction order should not matter, I want to formalize the state of a partially-solved puzzle as a collection of bits, initially all true. In map coloring, each bit could represent the possibility that a given cell is a particular color, and we want to eventually have one true bit per cell and the rest false. A deduction is a change to a single bit. Each deduction is triggered by a rule, which typically searches for certain patterns in the state. For instance, in map coloring, the pattern that one cell has only one remaining color whose bit is true can trigger the deduction that the same color’s bit in a neighboring cell must be false. Any given deduction could be triggered by more than one rule, or by more than one instance of the same rule. Then these rules and deductions should obey some natural properties:
-
The deductions can only go in one direction. If we deduce that a bit is false, we won’t later change it back to true.
-
The deductions are always valid for the intended puzzle. That is, when a puzzle has a unique solution, we won’t ever deduce anything inconsistent with that solution. (However, when that assumption is violated, anything can happen.)
-
It should be possible to efficiently identify all deductions that can be triggered from the current state. Ideally this should take polynomial time.
-
If a deduction is triggered by one of the rules, it remains triggered until that deduction step is performed.
I’m not assuming that the deduction system is complete, i.e., that it will reach the intended puzzle solution for all puzzles. For most natural puzzle types and most efficiently-searchable sets of deduction rules, it won’t be complete, and most likely (because of NP-completeness or related complexity issues) cannot be both complete and efficiently searchable. But nevertheless, a system of rules obeying these properties always reaches a unique state, independent of deduction order. It is the last of these properties that enforces this order-invariance. By induction on the values in the triggering patterns, each deduction that could be made by some order of deduction steps will eventually be made by a greedy algorithm that chooses deductions in an arbitrary order until it gets stuck.
The “remains triggered until performed” criterion should sound familiar. It is the defining property of an antimatroid, a collection of orderings of items (here, orderings of deductions that could be made by the greedy algorithm) with the property that once an item becomes available to be added to an ordering, it remains available until it actually is added. The antimatroid name is a bit technical and off-putting, but these structures come up all the time in many different applications. I’ve written here about listing all small antimatroids, visualizing their structure, algebraic axiomatization, hardness of finding weighted feasible sets, the swap structure on orderings, infinite antimatroids, informative comparisons, nearest neighbors, and the applications of antimatroids to pseudotriangulation, knot theory, computerized education, parts assembly, sorting networks, rhyme schemes, hereditary graph properties, course prerequisites, and hierarchical clustering. So why not add puzzle deduction to the list?
A nice side-effect of using deduction rules with these properties is that, if the rules are ordered by difficulty, then a greedy algorithm that always chooses the easiest rule at each step will automatically find a deduction sequence minimizing the difficulty of the hardest rule that it uses. This can be helpful in using deduction algorithms to automatically estimate the difficulty of a puzzle for a human solver.
A natural way to achieve the “remains triggered until performed” property for a deduction rule is to use a pattern in the form of a monotonic Boolean combination of state bits (a function that can be expressed using only Boolean and and or operations, without negation) and to trigger a deduction when that combination becomes false. In this way, we achieve a stronger property, that once triggered the deduction remains triggered forever (even after it has already been performed). But as we’ll see below, other kinds of rules can also have the same property.
Now back to map coloring.
We saw in my earlier post that it doesn’t work well to use rules like “if one cell has already-colored neighbors of two colors, and only one uncolored neighbor, then that neighbor cannot be either of the same two colors”. These rules are valid (under the assumption that the puzzle solution is unique) but lose information about why the deduction on the neighboring vertex was made, preventing later deductions from being made.
Instead, the insight I ended up using involves Kempe chains. A Kempe chain, in a colored map, is a maximal connected subset of the cells of two of the colors. If the coloring is to be unique, every Kempe chain must be anchored by one of the original givens of the puzzle, for otherwise we could swap the two colors in the chain without affecting the rest of the graph. So, I’ve started using rules of the form “if this Kempe chain in the partially colored map is not yet anchored, and can reach an anchor only by extending through this other cell, then that cell cannot be a third color”. Here, the Kempe chains that I examine to trigger this rule are maximal connected subsets of the cells whose colors are limited to some set of two colors, allowing cells that are already known to have only one of those two colors. Until we add the extension cell to the chain, the same rule will continue to be triggered, so this passes the any-order requirements above.
This deduction method also fits well into the visualization tools available for manual puzzle-solving in Simon Tatham’s puzzle collection, where I found the map puzzle. This collection’s implementation of the map puzzle shows the givens and solved cells as solid colors, and allows unsolved cells to be marked by dots of any combination of the four colors. So I’ve been using these dots to indicate the remaining colors available for each cell, in cases when the deductions get complicated enough that I can’t just remember them without marking them. A cell that has dots of only one color rather than a solid color is effectively solved (we know what color it is going to end up being) but might still belong to some unanchored Kempe chains. Once all three Kempe chains through a cell of known color have been anchored, I color that cell as solid. In this way, the parts of the solution that might include unanchored Kempe chains typically remain small and distinctively colored, making the chains easy to spot.
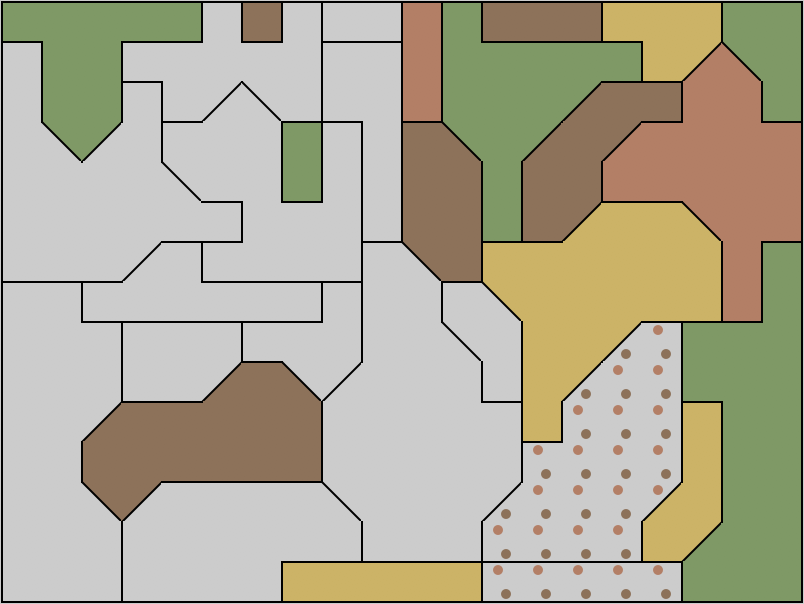
The image above shows an example, from one of the hardest built-in difficulty levels of the puzzle (“20x15, 30 regions, Unreasonable”). An orange-brown Kempe chain can be seen in the bottom left, in the two cells colored by orange and brown dots. (Yes, I know these two colors are hard to tell apart; I can’t change them.) Its only escape cell has yellow and brown neighbors, and cannot be green (leaving the orange-brown chain unanchored), so it must be orange. This set of deductions allows us in turn to infer the colors of the other two cells in the chain, and to make them solid (their three Kempe chains all become anchored). The orange escape cell becomes dotted rather than solid, because it is part of a different Kempe chain (colored orange-green) that remains unanchored.
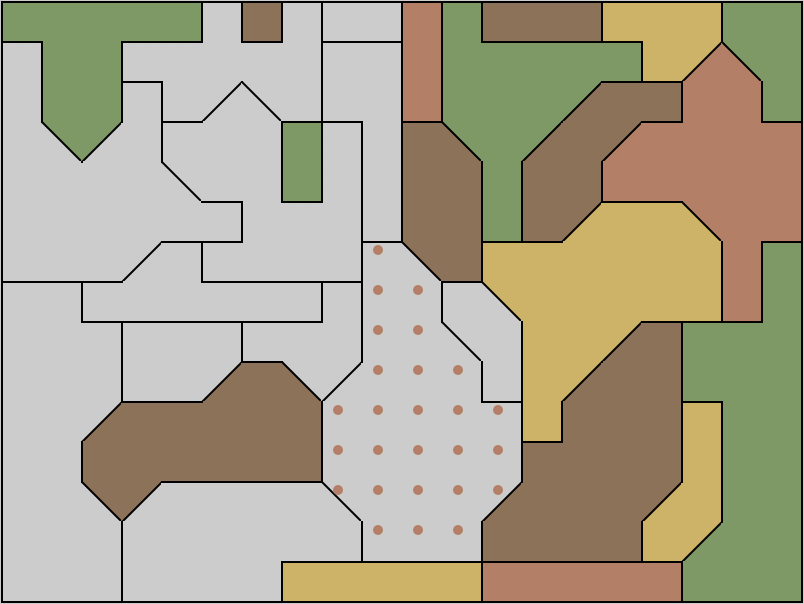
This extended deduction rule seems to be working well for the puzzles I’ve tried it on. And by obeying the requirement that deductions remain triggered until performed, it gives me confidence that I’m not hiding any usable information by doing my deductions in the wrong order. There is no wrong order: any order in which I make my deductions will eventually lead me to the same state.