Reverse search for antimatroids
An antimatroid (also called a learning space) is a family of sets closed under union, such that for every nonempty set in the family there is an element that can removed to produce another set in the family. It turns out that, for any antimatroid \( A \) except powersets, there is a set \( S \) on the same elements that can be added to \( A \) to make a larger augmented antimatroid.
Proof sketch: Let \( U \) be the union of the sets in \( A \), and by removing elements one at a time from \( U \) find \( T \) and \( x \) such that the sets between \( T \cup \{x\} \) and \( U \) form a powerset but the sets between \( T \) and \( U \) do not. If \( U \setminus \{x\} \) is in \( A \), then one can continue recursively in the subantimatroid between \( T \) and \( U\setminus \{x\} \); otherwise we can choose \( S \) to be a one-element extension of the largest set in \( A \) between \( T \) and \( U\setminus\{x\} \).
This proof can be turned into a deterministic algorithm for choosing a specific augmentation out of all the possible ones. If one considers the augmented antimatroid to be the parent of the original antimatroid, this parent relation forms a tree with the powerset at its root:
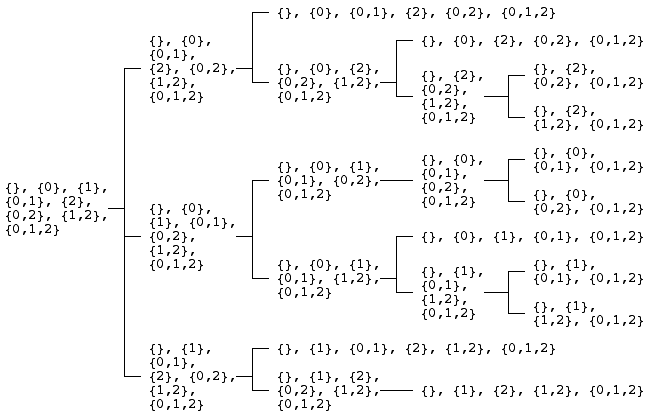
We can then generate all the possible antimatroids using reverse search, which is just a fancy phrase for an algorithm that explores a tree like this one by reversing the parent relation. The time per antimatroid generated, over a \( k \)-element universe, is polynomial in \( 2^k \), not bad since the number of antimatroids generated is double-exponential in \( k \).
I implemented this in Python, from which I generated the \( 22 \) families in the tree of \( 3 \)-element antimatroids above, matching some hand calculations I'd done previously. My program also found \( 485 \) antimatroids over \( 4 \) elements and \( 59386 \) over \( 5 \) elements, but I am a little distrustful of these numbers since the program is intricate and painful to debug. Unfortunately I couldn't find anything about this enumeration problem in the OEIS or with Google, so I'm at a bit of a loss for how to check these results; I suppose I could at least enumerate all \( 2^{16} \) \( 4 \)-element set families and test which ones are antimatroids.
If the pattern of number of antimatroids being roughly \( 2^{2^{k-1}} \) holds, the program as it stands should be able to list all \( 6 \)-element antimatroids in about a month of laptop time, but I suspect reimplementation in a faster language and/or running it on a faster machine should speed that up significantly, to closer to a single day.
ETA 6/19: This much shorter program for brute-force testing all \( 2^{16} \) \( 4 \)-element set families produces exactly the same output as my reverse search, so I am now much more confident in the reverse search results.
ETA2 6/20: Now up on the OEIS.