The 32-vertex graph shown below (with edges connected around the boundary of the drawing by matching pairs of letters) is an xyz graph in two different ways.

An ambiguous xyz graph

First, the paired letters can be seen as part of a torus embedding of the graph (in which the left and right ends are connected to each other, and the top and bottom ends are connected after a shift to form a brick wall pattern), and this torus embedding has 3-colorable faces, hence is xyz:

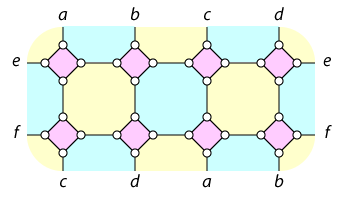
Torus xyz embedding of the ambiguous graph

But there is a less obvious embedding, in which the faces consist of zigzag paths through the drawing. In the shaded figure below, the blue faces zigzag from top left to bottom right, while the yellow faces zigzag from bottom left to top right. This embedding is related to the other one by applying a half-twist to each of the edges connecting two pink diamonds.

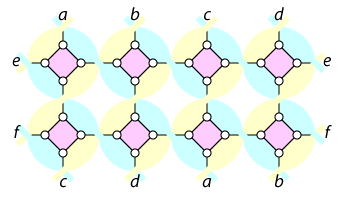
Twisted xyz embedding of the ambiguous graph

The second embedding also forms a torus (it has the same number of octagonal faces) and in fact both embeddings turn out to be isomorphic. That is, the graph has a hidden automorphism, that does not extend to an automorphism of its embedding on the torus, but instead gives a different embedding.

The same brick wall construction works with larger \(4k\times 2k\) arrays of diamonds. In each case there is an obvious torus embedding and a less obvious embedding formed by zigzag paths. But for the larger graphs, the two embeddings are not isomorphic: the zigzag paths are longer and fewer in number, so the nonobvious embeddings have higher genus. Graphs with arbitrarily large numbers of distinct embeddings or even arbitrarily large numbers of embeddings with different genuses are also easily constructed by connected sums of these graphs.

If every xyz graph had a unique representation as an xyz graph, that would be a hint to me that the problem of finding these representations could have a polynomial solution. But the existence of this sort of ambiguity makes me think that the problem could be \(\mathsf{NP}\)-complete, that perhaps somehow ambiguous graphs like this could be turned into gadgets in an \(\mathsf{NP}\)-completeness proof.