A conversation on the Secret Blogging seminar regarding axiomatizations for antimatroids led me to arXiv:0712.1047, an interesting paper on some connections between antimatroids and partial orders on the elements of Coxeter groups.

One of the constructions in the paper can be translated into computer science terminology in a way that I think may make it accessible to a larger (or at least different) audience. A sorting network can be formed in several different ways from \( n \) inputs and a set of comparators that take two adjacent inputs and output the same two values in sorted order. The following sorting network, for instance, describes the bubble sorting algorithm; I've drawn the comparators in an unconventional way, as circled crossings, to emphasize that either of the two inputs may end up on either of the two outputs.

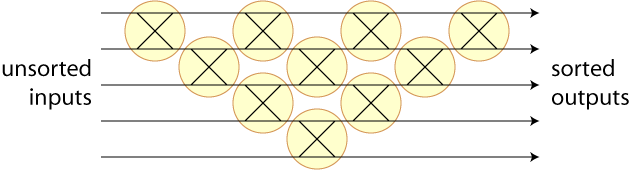
sorting network for bubble sort

More efficient sorting networks can be formed by connecting nonconsecutive pairs of inputs with comparators, but I'm less clear on the extent to which the results in the paper apply to those as well. If only consecutive pairs may be connected, and redundant comparators that never swap anything are disallowed, then there must be exactly \( n(n-1)/2 \) comparators: if one erases the straight connections through the comparators leaving only the crossed connections, the result is an arrangement of \( n \) \( x \)-monotone curves each of which crosses each other exactly once (that is, an arrangement of pseudolines).

Anyway, suppose we fix any one particular sorting network, such as the bubble sort network above. Different inputs will make different comparators within the network active, where we can define a comparator to be active if it swaps its two inputs. Consider the family of sets of active comparators produced by different inputs. There are \( n! \) different input orderings, each of which gives rise to a different set of active comparators, so this family of sets has \( n! \) different sets in it. For instance, if the input is already sorted, there will be no active comparators, so the empty set definitely belongs to this family. The illustration below shows another active set for a different input, with four active comparators. However just from counting the number of sets we can see that most sets of comparators cannot be made active in this way: there are only 120 possible input orders, so 120 different active sets out of 1024 possible subsets of comparators.

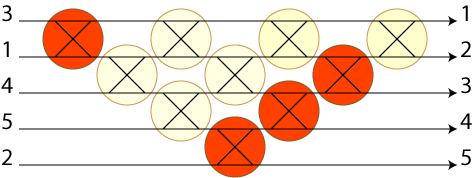
the active comparators for an input to bubble sort

A special case of the result in the paper, if I'm understanding it correctly, is: this family of sets forms an antimatroid! That is, if \( A \) and \( B \) are two active sets of comparators formed by two different unsorted inputs, then there's a third unsorted input that makes \( A \cup B \) active, and if \( C \) is a nonempty active set of comparators formed by any unsorted input then there's a transposition that can be made to that input that causes one fewer comparator to be active. In the case of the bubble sorting network this is easy to show directly (each active set has the form of a collection of diagonal stripes starting on the bottom left edge of the network and continuing upwards and to the right for any length, sets of this form are closed under unions, and one can make one fewer comparator active by shortening one of the stripes) but the result holds in much greater generality not only for all sorting networks of adjacent comparators but also for Coxeter group constructions involving groups other than the group of all permutations and generators other than the transpositions of adjacent pairs.

As an off-topic aside, for some reason it amuses me to see a remark such as the one in the first linked post's comment threads that antimatroids have “enough of a history to have a thorough Wikipedia page” without considering that some specific people (in this case, me) put some effort into causing that page to exist for idiosyncratic reasons and that other subjects with equally long histories have much more cursory representation in Wikipedia.