A zipless polycube
My latest arXiv preprint is “Some polycubes have no edge-unzipping” (arXiv:1907.08433, with Erik and Marty Demaine and Joe O’Rourke). It’s about polyhedral unfolding, the problem of cutting a polyhedron along some of its edges into a surface that unfolds into a flat polygon in the plane (a “net”). Although it dates back to the work of Albrecht Dürer, we still don’t know a lot about this problem, in general. We don’t know whether every convex polyhedron has an unfolding, and we don’t know whether every polycube has a folding (allowing cuts in the middle of flat faces as long as they are on boundary edges of the cubes making up the polycube).
The preprint is about a variation of unfolding in which the cut has to form a path through the graph of vertices and edges. If the polyhedron has the topology of a sphere and there are no flat vertices (with a full \(2\pi\) total angle of surrounding faces) then all vertices must be touched by a cut, and it’s the same thing to ask for an unfolding that forms a Hamiltonian path. These zipper-unfoldings have previously been studied, notably in joint work by two parent-child groups, Marty and his son Erik, and Anna Lubiw and her two sons Arlo and Jonah from CCCG 2010. The new preprint shows that they don’t always exist for (topologically spherical) polycubes. In particular, the following shape has no flat vertices, but its graph is bipartite and unbalanced enough that it also has no Hamiltonian path.

It does have an unfolding, though (figure made by Erik using OrigamiSimulator):
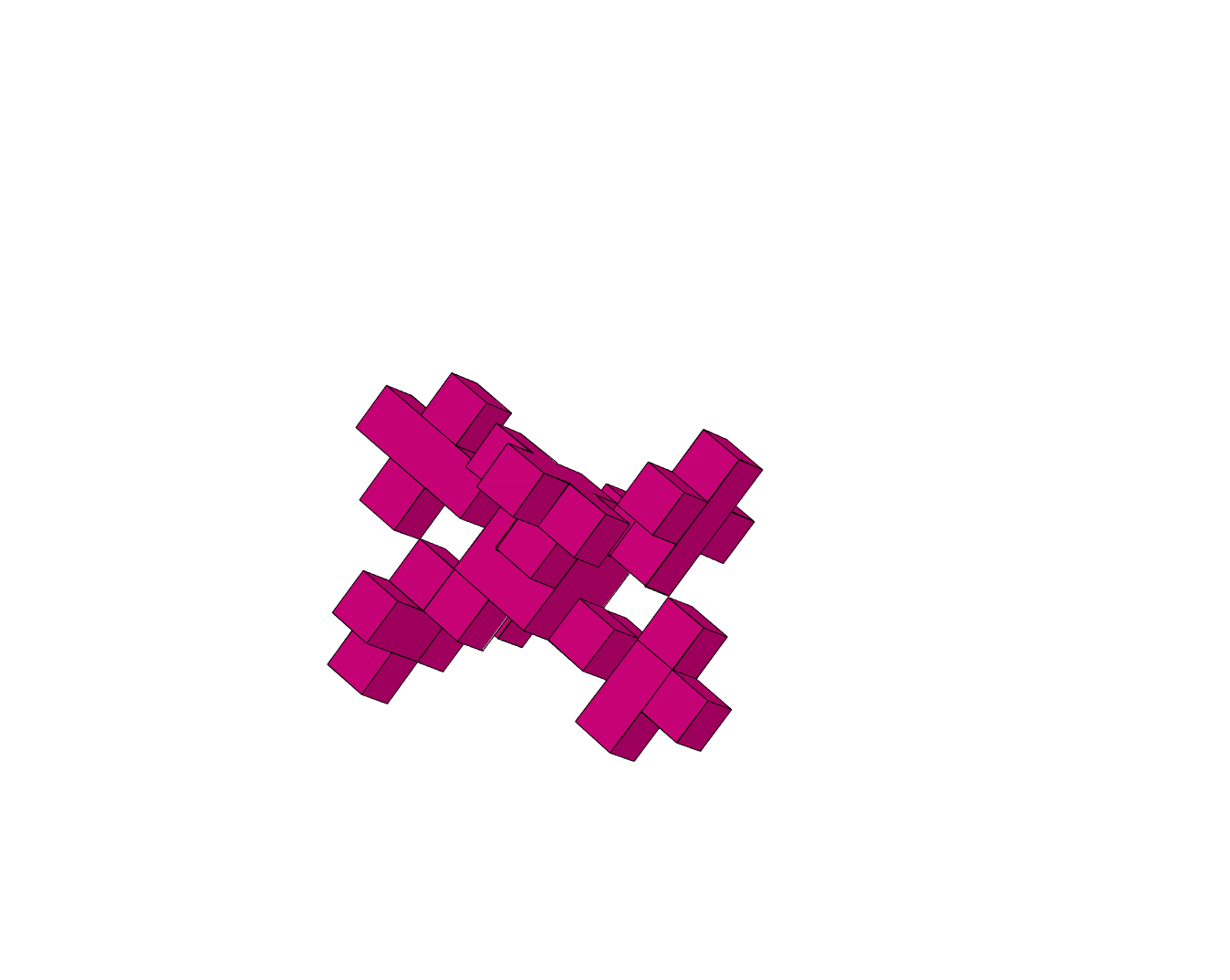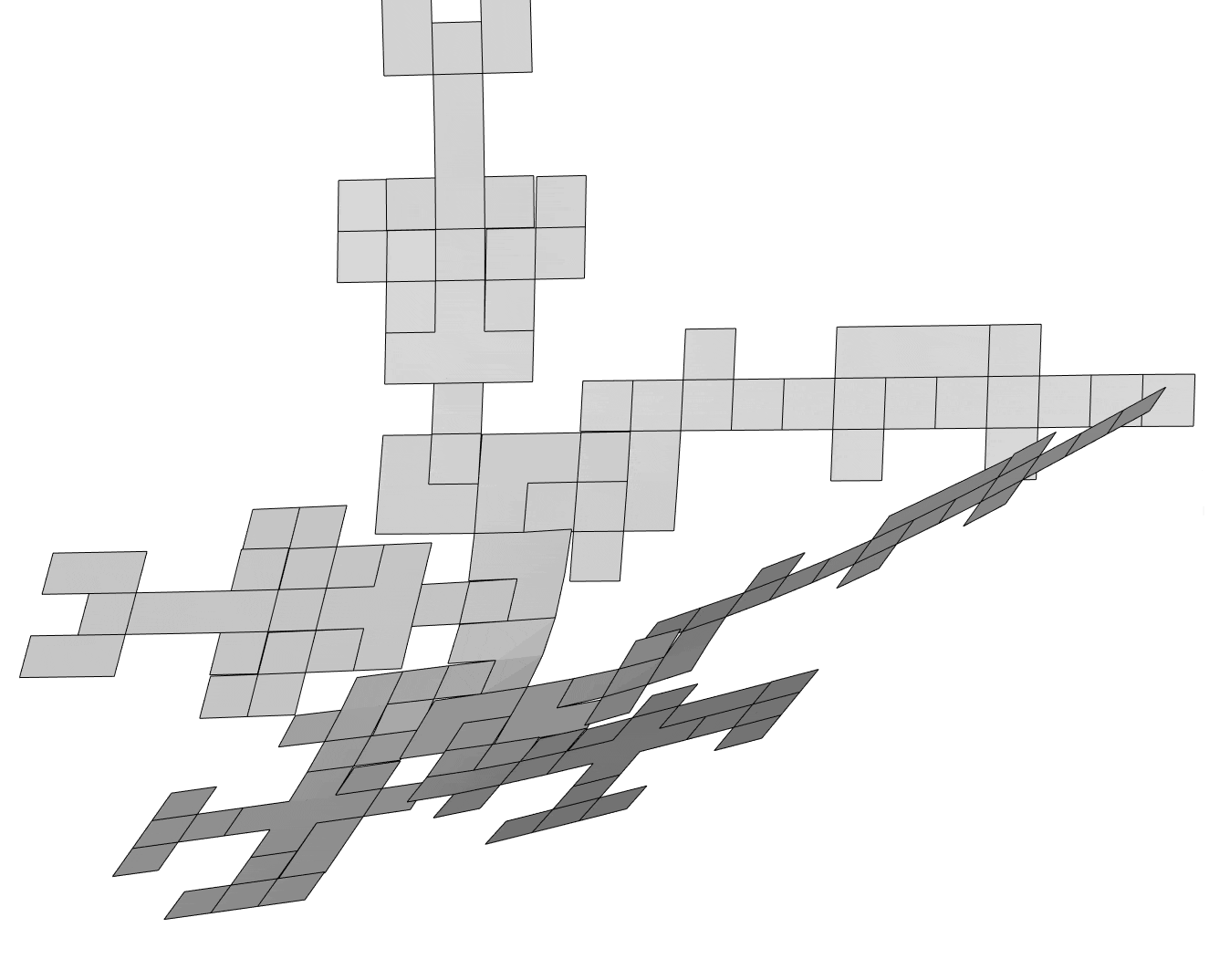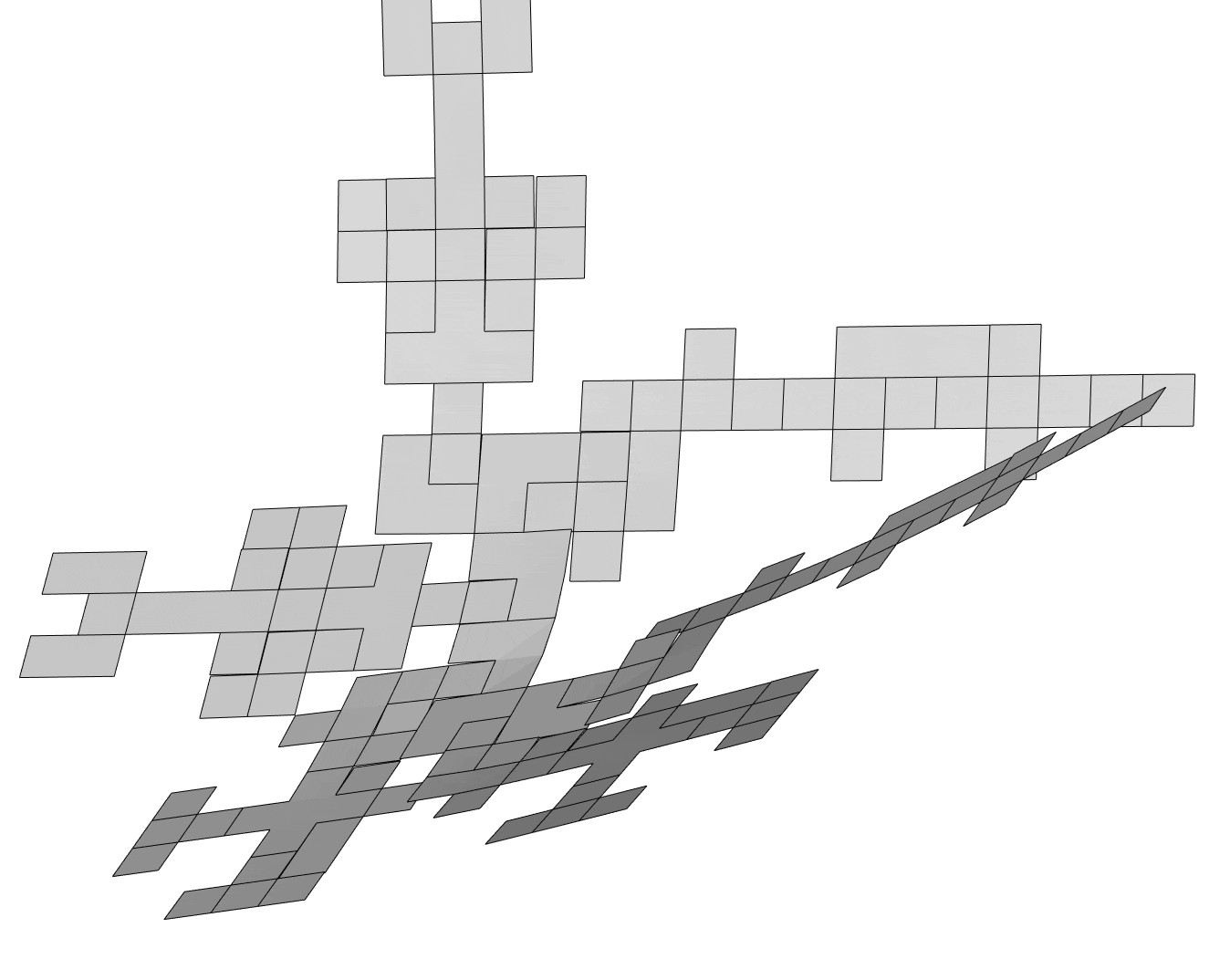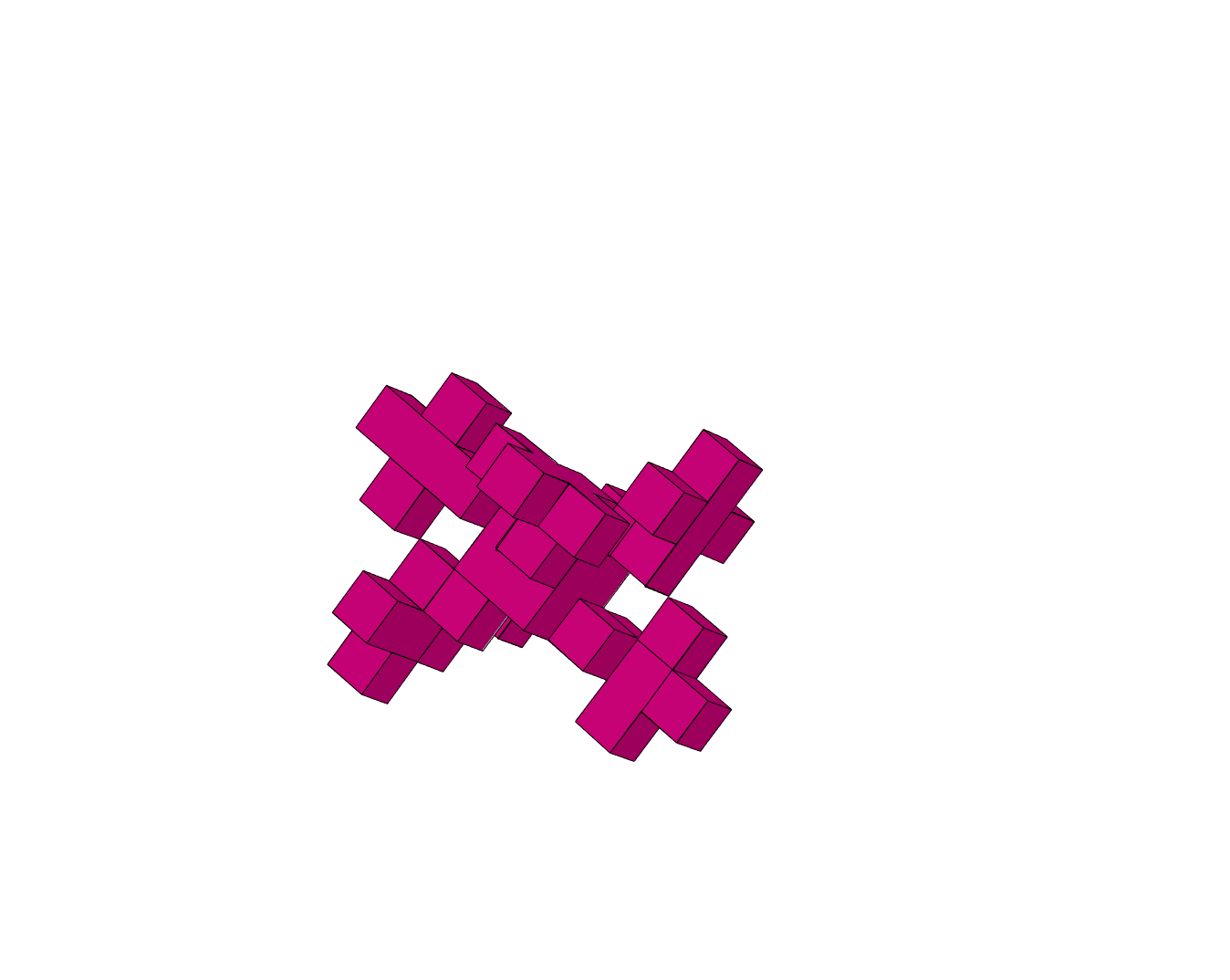
The paper also has a smaller example that’s a little tricker to prove zipless. It’s a small enough advance that we probably won’t bother trying to turn it into a conference or journal paper. (If it were just me, I’d probably have just made a blog post about it. And here we are!)