Local and inductive properties of graphs

At LATIN, Allan Borodin brought my attention to a recent paper of his with Yuli Ye, "Elimination graphs" (TALG 2012), about an idea that combines local properties of graphs with degeneracy.

For a graph property \( P \), a graph \( G \) is "locally \( P \)" if the open neighborhood of each vertex \( v \) in \( G \) (the subgraph of \( G \) induced by the neighbors of \( v \)) has property \( P \). For instance, a graph is locally cyclic if every vertex's neighbors induce a cycle; these are the graphs of certain well-behaved surface triangulations (every clique of the graph is a simplex in the triangulation). In the hecatohedron below, every neighborhood is a 5-cycle or a 6-cycle.

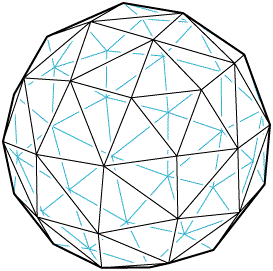
Local graph properties work particularly well when \( P \) is hereditary (that is, when induced subgraphs of graphs with property \( P \) also have property \( P \)). For then the property of being locally \( P \) is also hereditary. And, in this case, being locally \( P \) is a generalization of being \( P \). For instance, the claw-free graphs are exactly the locally 2-independent graphs (every neighborhood has independence number at most 2); being 2-independent and being claw-free are both hereditary. The graphs of bounded degree are exactly the locally bounded graphs (every neighborhood has constant size).

Analogously, Borodin and Ye define an undirected graph to be "inductively \( P \)" if its vertices can be ordered into a sequence so that, for each \( v \), the graph induced by the earlier neighbors of \( v \) in the sequence has property \( P \). Again, this works particularly well when \( P \) is hereditary, because then being inductively \( P \) is also hereditary and generalizes P. Additionally, when \( P \) is hereditary, the set of orderings in which the vertices can be removed (before reversal) forms an antimatroid, and a valid vertex ordering can be found by a greedy algorithm that repeatedly removes a vertex from the given graph whose neighbors have property \( P \). This algorithm can remove all vertices if and only if the graph is inductively \( P \), in which case the inductive ordering is the reverse of the removal ordering. Therefore, whenever \( P \) is hereditary and can be tested in polynomial time, so can the property of being inductively \( P \).

With this definition, a graph has bounded degeneracy if and only if it is inductively bounded, with the degeneracy equal to the largest earlier-neighborhood size in an ordering that minimizes this size. A graph is chordal if and only if it is inductively complete (inductively 1-independent), and the inductive ordering in this case is called an elimination ordering. In this way, Borodin and Ye formalize a common generalization of degeneracy orderings and elimination orderings. However, another standard type of vertex ordering, a perfect ordering, can't be defined via inductive hereditary properties, because the orderings are NP-hard to find.

The particular property most closely examined by Borodin and Ye is that of being inductively \( k \)-independent, which generalizes chordal graphs (\( k=1 \)), degenerate graphs (\( k={} \)degeneracy), claw-free graphs (\( k=2 \)), planar graphs (\( k=3 \), beating the degeneracy bound of 5), unit disk graphs (\( k=3 \)), and disk graphs more generally (order by radius to get \( k=5 \)). With this property, for instance, a greedy coloring in the inductive order uses at most \( k \) times the optimal number of colors (because any coloring of the earlier neighborhood of any vertex uses at most \( k \) times the number of colors that would have been used in an optimal coloring). They also show that the inductively \( k \)-independent graphs have \( (k+1) \)-approximations to their maximum weighted independent set.

Borodin and Ye give a time bound of \( O(n^{k+2}) \) time for recognizing inductively \( k \)-independent graphs, or \( O(n^{k+3}) \) in linear space, when \( k \) is a constant. They list improving these time bounds as their most important open problem. Here, some observations already used for recognizing claw-free graphs may help. For instance, each removed vertex can have only \( O(\sqrt{m}) \) neighbors (else its neighborhood would be too sparse to be only k-independent), an observation made in the claw-free case by Kloks, Kratsch & Müller (2000). And, when seeking a vertex to remove, only \( O(\sqrt{m}) \) of them can even have this many neighbors. This immediately improves the linear-space algorithm to \( O(nm^{(k+2)/2}) \). It seems likely that the fast matrix multiplication methods used to speed up claw-free graph recognition can also be used here to reduce the exponent (as Borodin and Ye already do for some small values of \( k \)), but I haven't worked out the details. On the other hand, one can't do much better, because a graph \( G \) has independence number at most \( k \) if and only if the graph formed from \( G \) by adding \( k+1 \) independent new vertices, each adjacent to all the original vertices, is inductively \( k \)-independent. Therefore, inductive \( k \)-independence is no easier than \( k \)-independence, and (under the exponential time hypothesis) it requires an exponent linear in \( k \) by results of Chen et al. (2006).

---

Comments: