Recognizing sparse leaf powers
I’ve written about Courcelle’s theorem here several times before. It’s a powerful “algorithmic meta-theorem” that lets you turn a logical characterization of a graph property into an algorithm for testing the property that runs in linear time in the input graphs size, for graphs of bounded treewidth. Unfortunately the constant factor of the linear time bound depends badly on the treewidth. In past posts, I’ve used this to formulate algorithms for minimal-crossing book embeddings, graph toughness, splitting vertices to make graphs planar, finding \(k\) shortest paths, and constructing clustered planar drawings. My latest preprint, “Parameterized Leaf Power Recognition via Embedding into Graph Products” (arXiv:1810.02452, with UCI student Elham Havvaei, to appear in the proceedings of IPEC 2018) applies the same method to the problem of recognizing leaf powers.
A \(k\)-leaf power is a graph formed from a tree by keeping only the leaves of the tree as vertices, and connecting two leaves by an edge if their tree distance is at most \(k\). Here’s an example of a tree and the corresponding \(3\)-leaf power that I drew for the Wikipedia article a couple of years ago, before this paper existed.
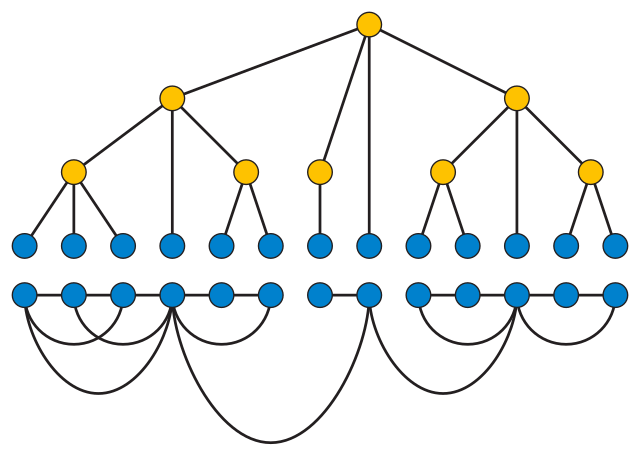
It’s not hard to formulate in logic the condition that a certain set of edges \(T\) must form a tree, or that each edge of the given graph must correspond to a path of length at most \(k\) in \(T\) (at least, when \(k\) is a fixed constant rather than allowed to vary). But this doesn’t work directly for leaf powers. The problem is that the tree has vertices and edges that don’t exist in the leaf power: the internal vertices of the tree, and all of the edges adjacent to them (which is all of the edges in the tree). But to apply Courcelle’s theorem, we need to express everything in terms of vertices, edges, and sets of vertices and edges of the input graph, and the input graph is the leaf power, not the tree. I’m pretty sure it’s still possible in this case, but the details are messy, and eluded us until we came up with the following trick.
When we’re developing an algorithm using Courcelle’s theorem, the graph that we apply the logical formulation to doesn’t need to be the input graph of the algorithm. Instead, it can be any other graph that we can compute easily (and still has small treewidth). In the case of \(k\)-leaf powers, it turns out to work to use a graph that’s a product of a \(k\)-vertex cycle with the input graph. If the input is really a leaf power, the tree that it comes from can be embedded into this product graph. The logical formulation of this embedding is much simpler than the formulation of leaf powers in terms of the original graph (assuming such a formulation exists). And the product by a cycle only blows up the treewidth by a factor of \(k\), not a problem given that we already were going to have a horribly impractical dependence on the treewidth.
Instead of treewidth, our paper parameterizes its dependence on the graph structure using degeneracy, a measure of how sparse the graph is rather than of how tree-like it is. But in this case, going from one parameter to the other is not difficult. The \(k\)-leaf powers are known to have bounded clique-width, and the graphs of bounded clique-width and bounded degeneracy are known to have bounded treewidth. So if we get a sparse graph whose treewidth is too big, we can bounce it immediately as not being a \(k\)-leaf power, and otherwise we can apply techniques such as Courcelle’s theorem that are based on treewidth.
As we note in the conclusions, this technique would also have greatly simplified the application of Courcelle to the problem of splitting vertices. It’s also possible that it could lead to more practical algorithms. In another earlier posting I mentioned Max Bannach’s and Sebastian Berndt’s best student paper of ESA 2018 track B, “Practical access to dynamic programming on tree decompositions”. Part of their paper involves finding constrained fragments of second-order graph logic for which Courcelle’s theorem can be implemented more efficiently. Our graph product technique may help in this respect, by simplifying the logical formulation (of the problems on which it works) far enough to allow Bannach’s and Berndt’s implementation methods to apply.