Linkage

Because Google+ has been scheduled for shutdown (see item below), I’ve started cross-posting links to my Mastodon account @11011110@mathstodon.xyz in the hope that this gives me a smooth transition plan when the shutdown occurs. It also lets me put math formulas into my posts! Those new cross-posts are where the little \(\mathbb{M}\) links on some of the entries below go. So if you want to see these postings when I make them, rather than these later roundups, follow me there.

• Crooked Timber on algorithms (G+). This piece on algorithmic decision-making makes the point that the kind of “algorithm” used for these tasks is very different from the historical meaning of the word, and that these methods are likely to fall into the same errors that have painstakingly been weeded out from more principled statistical methods in social science and economics.

• More than 9 million broken links on Wikipedia are now rescued (via). The internet archive continues to be extremely useful, in this case for rescuing broken links from Wikipedia articles. (I’m also a big fan of its collection of out-of-copyright books.)

• Twenty geometry puzzles by Catriona Shearer on Math with Bad Drawings (via). I like the ones from this set where you can get the answer with a quick flash of insight and very little calculation. The one below is one of those. Or maybe they all are, and I just haven’t found the insights for all of them?

• The generative art of Manolo Gamboa Naon (G+).

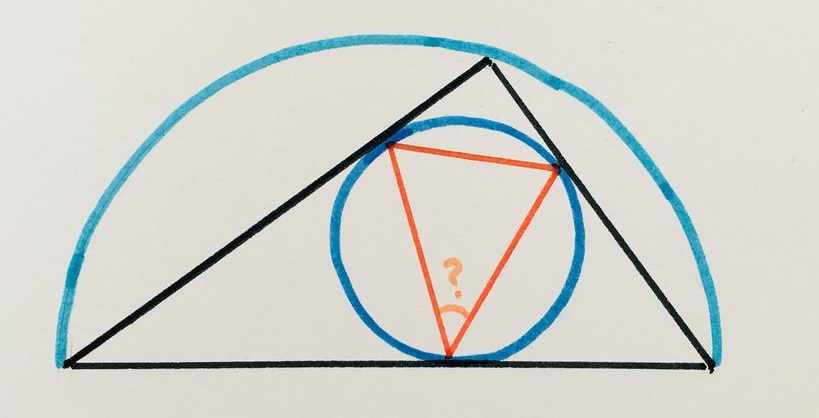
• Quotable women in mathematics. Taken from interviews with seven mathematicians at the Heidelberg Laureate Forum, now on Wikiquote thanks to Katie Steckles.

• A UW professor argued that women don’t want to code. What do women computer scientists have to say? (G+). Responses to Stuart Reges’ claims that most discrimination is gone and most of the remaining gender gap is innate, by three U. Washington professors and three current and former students.

• Google is shutting down Google+ following security lapse (G+, more G+ comments, \(\mathbb{M}\)). As I wrote on G+, this makes more urgent the need for me to find a better way to hold discussions online. Facebook is for personal friends and family only. Twitter makes conversations hard to follow, is overrun by robots and spammers, and welcomes nazis at its highest levels while shutting down left-wing academics. For now I’m going with Mastodon, but see the G+ post for more discussion.

• The list of accepted papers at SODA 2019, the annual ACM–SIAM conference on discrete algorithms, to be held next January in San Diego (\(\mathbb{M}\), via).

• Bonus link for Mastodon only! Andrew T. plays at generating snowflakes using cellular automata. Mastodon doesn’t seem to have a way to link to a boost of a post separately from the post itself, so I only have a direct link to Andrew’s post.

• A new ACO Center (\(\mathbb{M}\)). Vijay Vazirani on the new “algorithms, combinatorics, and optimization” center he’s been organizing at UC Irvine, connecting researchers in CS, mathematics, and the business school, and modeled after the success of similar programs at CMU and Georgia Tech.

• A problem fit for a princess (\(\mathbb{M}\)). A post on the history of the Apollonian Gasket, a fractal formed by tangent circles, inspired by its use as the logo of the San Joaquin Math Teachers’ Circle.

• Amazon trained a sexism-fighting, resume-screening AI with sexist hiring data, so the bot became sexist (\(\mathbb{M}\)). Merely having the intention of using automation to eliminate discrimination isn’t good enough, especially when machine-learning-based decision systems are clever at finding seemingly-innocuous data that allows them to replicate past discrimination.

• Hand-drawn Delaunay Triangulation and Voronoi Diagram overlay (G+, \(\mathbb{M}\)). Four in-progress views by Del. Doing the Delaunay part first does seem like the right way to do it, even if what you want is only the Voronoi diagram, since that way the triangles guide you in making the bisectors meet in the right places. Some of the dual pairs of edges seem a bit non-perpendicular in this example, though…

• Graduate student solves quantum verification problem (G+, \(\mathbb{M}\)). Quanta Magazine on Urmila Mahadev’s interactive protocols for testing whether a supposedly-quantum computer is really doing quantum stuff, and her persistence at solving this problem when she could easily have completed her Ph.D. with what she already had done.

• On the number of points in general position in the plane (\(\mathbb{M}\)). Balogh and Solymosi’s new paper constructs \(n\) points in the plane, no four in line, with max general-position subset size \(O(n^{5/6+\epsilon})\), much better than the previous \(o(n)\). I recently rescued a Wikipedia article on Solymosi from the draft namespace where it was languishing, adding book references for his results, but I left out my favorite (this one) because it wasn’t published. Now it is, but the book reference would be too self-serving to add…