I've been playing with the Cayley graphs of the symmetric group again, after accidentally running across the Wikipedia article on the icositruncated dodecadodecahedron and thinking "oh yeah, that's the polyhedron that geometrically represents the Cayley graph generated by a transposition and a 4-cycle".

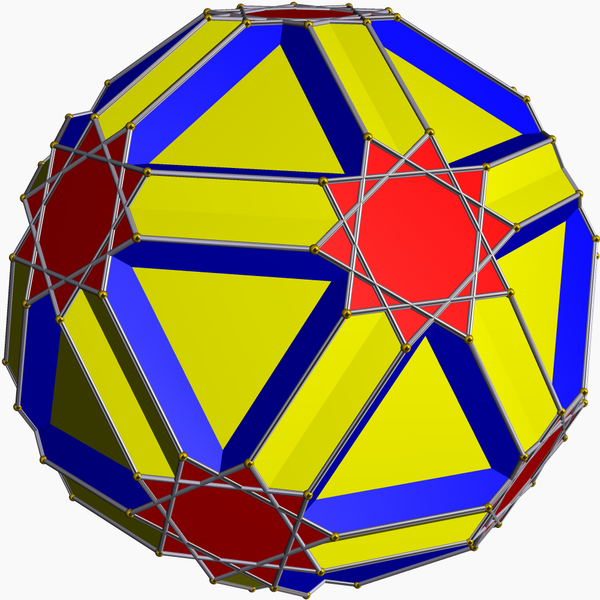
Icositruncated dodecadodecahedron created by Stella, from File:Icositruncated dodecadodecahedron.png on Wikimedia commons

Only, it's not. That was a different star polyhedron. So is the icositruncated dodecadodecahedron also a permutohedron? And if so, what are the generators of the corresponding Cayley graph?

To begin with, there are two different ways to form 3-regular (undirected) Cayley graphs. You can start with two generating permutations, one of which is self-inverse (an involution), or you can start with three generators, all three of which are involutions. In either case, the vertices are all possible permutations and the edges tell you which permutation you get when you multiply another permutation by a generator.

Both of these constructions give rise not just to a graph but a topological surface, made out of three sets of polygons. In the two-generator case, one of the three sets of polygons are the cycles that you get by repeatedly applying the non-involution generator, and the other two are cycles that alternate between two generators. In the three-involution case, all three sets of polygons are formed by alternating between two out of three of the generators. What I really want to know is not just whether I have the right graph, but also whether I have the right sets of polygons (the red, blue, and yellow ones in the picture).

First, let's consider the case that we have three involutions. You can visualize an involution as a matching on a set of vertices, so three involutions can be visualized as a 3-edge-colored multigraph on these vertices, and two out of three of them will form some kind of partition of the vertices into alternating paths and cycles. In the case of the icositruncated dodecahedron, two of the three sets of polygons are decagons (\( 2n \)-gons, where \( n=5 \) is the number of things being permuted). A little thought should convince you that in this case the corresponding two involutions have to form a single \( 5 \)-vertex alternating path; otherwise there is no way of getting a factor of five into the order of the group they generate. So we have three involutions, two pairs of which form alternating paths. There are five combinatorially distinct ways of doing this, two of which cause the other pair of involutions to generate a \( 6 \)-cycle:

The five combinatorially distinct involutions on five items in which two pairs of involutions form an alternating path on all five items

(The one labeled "10,10,10B", a \( 3 \)-edge-coloring of the complete bipartite graph \( K_{2,3} \), has symmetries taking any color class to any other color class, and so should result in an especially symmetric Cayley graph.) But none of these generate the icositruncated dodecadodecahedron, nor do they generate the symmetric group. The reason is that all three generators have an even number of transpositions, so they all belong to the alternating subgroup of the symmetric group. (Sometimes a proper subgroup; for instance 10,10,10A is the dihedral group.) That means that we get at most \( 60 \) vertices, not \( 120 \), when we generate the Cayley graph of these generators and its corresponding system of polygons, giving us some other (abstract) polyhedron than the one we wanted.

Ok, how about one involution and one non-involution? There, things work a bit better. Suppose that \( g \) is a permutation on a set of elements, consisting of two disjoint cycles of lengths \( x \) and \( y \), and that \( h \) is an involution that transposes one pair of elements from one cycle to the other. Then it turns out that the product of these two permutations is a cycle on \( x+y \) elements, so \( g \) and \( h \) generate a transitive group. By composing \( h \) with powers of the cycle, we can find many other transpositions, enough that whenever \( \gcd(x,y) = 1 \) we get the whole symmetric group. The sizes of the polygons in the Cayley graph generated by \( g \) and \( h \) are \( 2(x+y) \) (for the polygons that alternate between the two generators) and \( xy \) (for the polygons generated by \( g \) alone).

Choosing \( (x,y)=(1,n-1) \) gives us the Cayley graphs from the previous post, generated by a transposition and an \( (n-1) \)-cycle. But choosing \( (x,y)=(2,3) \) gives us the cycle lengths of \( 6 \) and \( 10 \) that we want, in a genuine Cayley graph of the symmetric group. Is it the same as the graph of the polyhedron? I'm not sure, but I strongly suspect that it is.

The good folks at Gödel's last letter have a habit of ending their posts with open problems, so here's one: this construction using a two-cycle permutation and a transposition gives a big class of \( 3 \)-regular graphs, in which the cycles that we know about can be made quite large. (Of course there could be other, shorter cycles.) Regular graphs in which all cycles are sufficiently large (larger than this) are automatically good expander graphs. Do some or all of these \( (x,y) \)-Cayley graphs also have good expansion?