Surfaces for symmetric groups
Inspired by my previous post on a truncated-cube Cayley graph for permutations on four elements, I tried looking at similar presentations for larger permutation groups.
In the permutation group \( S_n \) on \( n \) items, let \( x \) denote the operation that swaps the first two elements of a permutation, and \( y \) denote the operation that rotates the remaining \( n-1 \) elements. Then \( xy \) rotates all \( n \) elements by one position, so these operations satisfy the relations \( x^2=1 \), \( y^{n-1}=1 \), and \( (xy)^n=1 \). One can transpose any two adjacent elements by a composition of these operations of the form \( xy)^kx(xy)^{n-k} \), so \( x \) and \( y \) generate the whole symmetric group.
The group presentation \[ \bigl\langle x,y \mid x^2, y^{n-1}, (xy)^n \bigr\rangle \] can be interpreted for \( n\gt 4 \) as defining a tiling of the hyperbolic plane by \( (n-1) \)-gons and \( 2n \)-gons, meeting at vertices with one \( (n-1) \)-gon and two \( 2n \)-gons per vertex. Since this is an infinite tiling, the group presentation defines an infinite Cayley graph of an infinite group, but \( S_n \) is a quotient of this group, and inherits from it a structure as a Cayley graph embedded on a manifold. This embedded Cayley graph for \( S_n \) has the same types of vertices and faces as the hyperbolic tiling, but finitely many of them.
When \( n \) is even (as in the case of the truncated cube for permutations on four items) the \( (n-1) \)-gons of this surface embedding form odd faces, preventing the surface from being an xyz surface in the sense defined in my recent paper. But when \( n \) is odd, we do get an xyz surface, as we may three-color the faces of the embedding. The \( (n-1) \)-gons all get a single color. Each \( 2n \)-gon consists of the \( n \) cyclic rotations of some permutation \( \pi \), together with a set of \( n \) additional permutations that are not cyclic rotations of each other; we may choose \( \pi \) to be the permutation among these cyclic rotations that fixes the first element. With this choice, we can describe the \( 2n \)-gons that are adjacent to the \( 2n \)-gon defined by \( \pi \): they are formed either by transposing adjacent pairs of elements in π other than the first element, or by applying \( y^{-1} \) to \( \pi \) and cyclically rotating the elements other than the first. When \( n \) is odd, each of these operations changes the parity of the permutation representing the cycle, so the adjacency structure of the \( 2n \)-gons is bipartite and we may two-color these faces.
We may determine the surface formed by \( S_n \) by checking the bipartiteness of the Cayley graph and the Euler characteristic of the surface. \( S_n \) forms a bipartite Cayley graph when \( n \) is odd (as each operation changes the permutation parity) and not when \( n \) is even (as the cycles \( y^{n-1} \) are odd). It has \( n! \) vertices, \( \frac{3}{2}n! \) edges, \( n!/(n-1) \) \( (n-1) \)-gonal faces, and \( (n-1)! \) \( 2n \)-gonal faces.
For instance, for permutations on 5 elements, we get a nice map on a genus-4 oriented surface with 120 vertices, 180 edges, 30 quadrilaterals, and 24 decagons. It is the truncation of an even nicer map, with 30 vertices, 60 edges, and 24 pentagons meeting four pentagons per vertex. Geometrically, the surface for the Cayley graph of \( S_5 \) also appears to be the graph-encoded map (GEM) of the small stellated dodecahedron or great dodecahedron, and to be represented itself geometrically as the truncated_dodecadodecahedron:
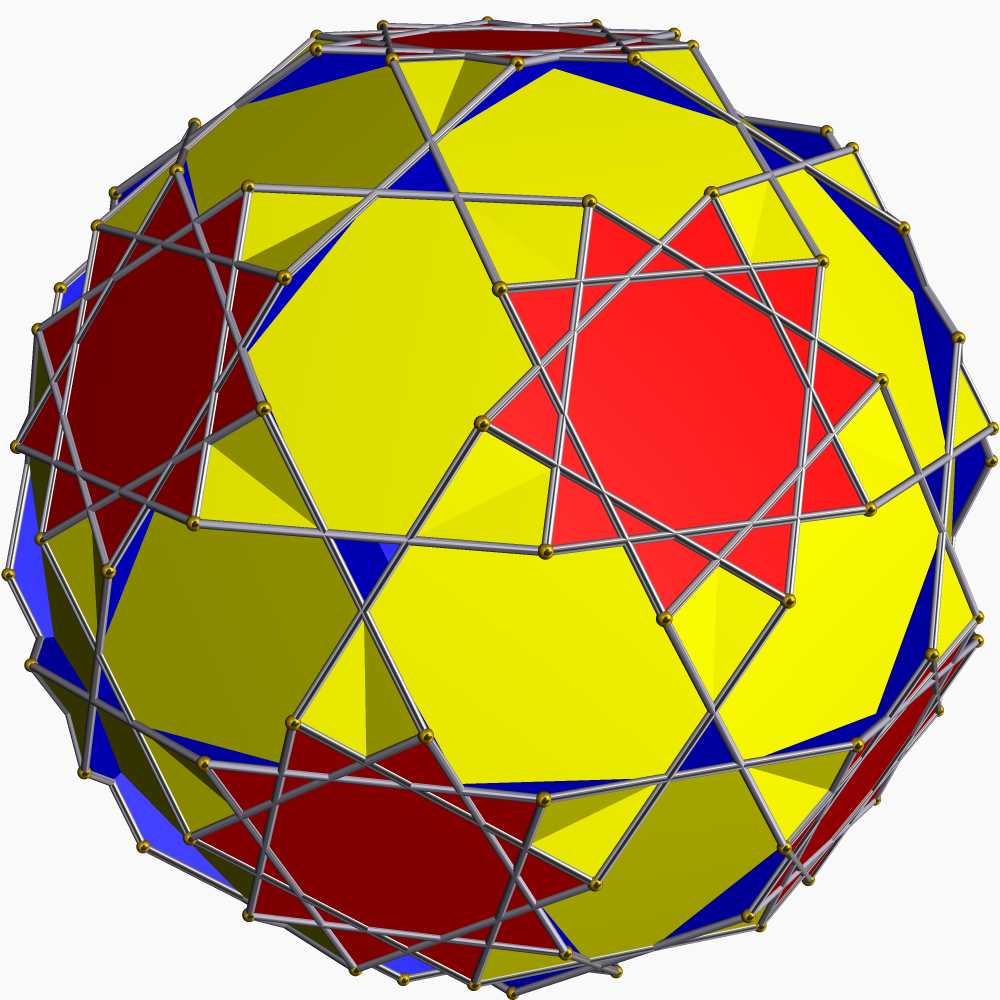
(This image, copied from Wikipedia, is by Robert C. Webb.)
In this geometric representation, the xyz-surface faces' 3-coloring is clear: we have yellow squares, large blue decagons, and small red 10/3 stars.