I have another preprint on the arXiv: “Combinatorics and geometry of finite and infinite squaregraphs” (arXiv:0905.4537), with Hans-Jürgen Bandelt and Victor Chepoi. It's a long one, 46 pages, and as the title says is about the properties of squaregraphs, planar graphs in which all the interior faces are quadrilaterals and all the interior vertices have degree at least four.

About a year ago I made several postings here about chord diagrams, the patterns formed by multiple chords in a circle (or, if you like, simple line arrangements in the hyperbolic plane). Now I can explain why: it's because of this paper. As I described here, if one has a hyperbolic line arrangement with no three mutually intersecting lines (a chord diagram with no ...a...b...c...a...b...c... pattern), its planar dual is a squaregraph, and all finite squaregraphs can be constructed in this way.

Coloring the chords of a chord diagram (so that no two chords of the same color cross each other) corresponds to embedding a squaregraph into a Cartesian product of trees. It's possible to give the vertices of a tree constant-sized labels in such a way that one can in constant time determine the distance of two vertices by looking at their labels, and this coloring idea allows the same distance labeling techniques to be applied to quadtrees, but with a label size that depends on the number of trees in the Cartesian product, or equivalently on the number of colors in the coloring. The squaregraph dual to Ageev's 5-chromatic chord diagram shows that this sort of labeling scheme sometimes needs as many as five trees, but never more than that.

Here's another curious fact about squaregraphs that we needed as a lemma, and is vaguely related to my recent post about visualizing breadth-first search: if one performs a BFS on a squaregraph, starting at any vertex, it's always possible to connect each level of the BFS tree into a cycle, and draw these cycles concentrically around the starting vertex, in such a way that the cycle edges don't cross the squaregraph edges. That is, in graph drawing terminology, the cycles and the squaregraph have a simultaneous embedding.

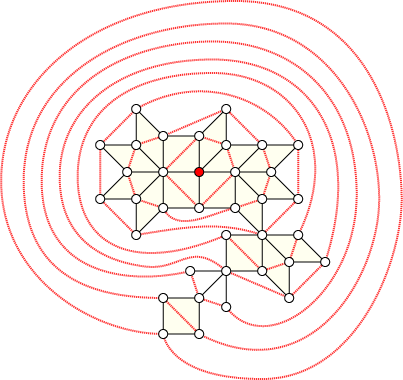
Concentric cycles formed from a breadth-first search of a squaregraph

Exercise: find a planar bipartite graph \( G, \) and a starting vertex \( v, \) such that the levels of the BFS tree rooted at \( v \) cannot be connected into cycles and simultaneously embedded with \( G. \)

There's also lots more in the paper about forbidden subgraph characterizations of squaregraphs, algorithms for finding small sets of vertices that generate the whole graph by median operations, infinite squaregraphs and their duality relation with infinite hyperbolic line arrangements (a little messier than we had hoped: duals of hyperbolic line arrangements can be disconnected, and connected duals of hyperbolic line arrangements aren't general enough; but a general class of infinite squaregraphs is formed by the connected components of duals of infinite triangle-free hyperbolic line arrangements), etc.