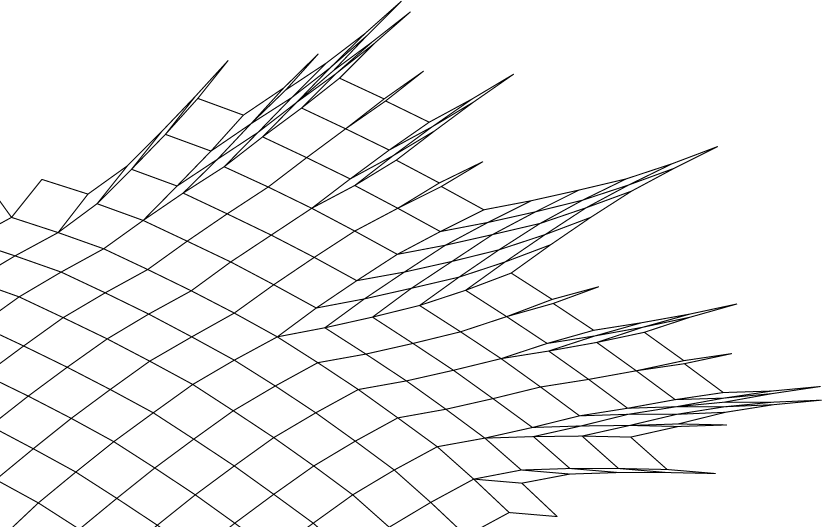
Ageev's squaregraph

A. A. Ageev, in his paper "a triangle-free circle graph with chromatic number 5" [Discrete Math. 152: 295–298, 1996], constructed a chord diagram with 220 chords that needs five colors in any coloring for which crossing chords are given different colors; this is the maximum possible number of colors needed for any triangle-free chord diagram. The dual graph of Ageev's arrangement is a large squaregraph. Using the labeling scheme from my previous post together with some drawing algorithms from one of my papers, I was able to draw it, with each face drawn as a rhombus:

Since the diagram is hard to view near the edges where the rhombi get very sharp, here's a blowup of one of its five lobes. The other four are symmetric.

ETA: the chord diagram itself, drawn as a hyperbolic line arrangement. I'll leave 5-coloring it as an exercise...

---

Comments: