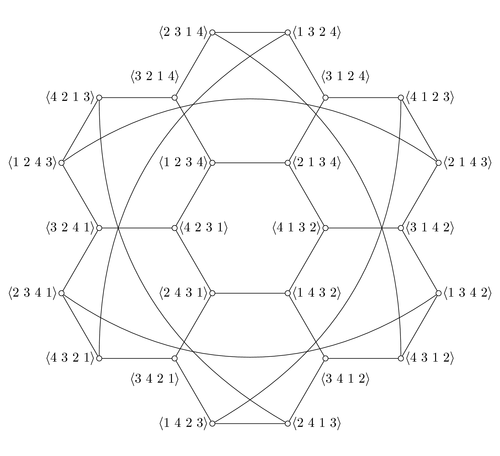
Yet another drawing of the Nauru graph
I've previously posted about drawing this graph, the unique 3-regular 24-vertex symmetric graph, here, here, and here.
Today a co-author pointed me towards tikz, a package for drawing things in TeX. And what do I find as the most recently posted example? The same graph, drawn in yet another way. They call it the "star graph", but (1) that's the name for the infinite family of Cayley graphs of Sn to which it belongs, and (2) it's a bad name because a star is also a tree with one non-leaf node; the Cayley graphs have as generators a set of swaps forming a star tree. Anyway, their drawing is pretty close to my drawing of it as a hexagonal torus tiled with smaller hexagons, but with the wraparound torus edges drawn across the planar part. For comparison, here are the tikz image and my image: