Topology of xyz graphs
For lack of a more creative name, I've decided to call the graphs I discussed a couple days ago, formed from point sets intersecting any axis-parallel line in zero or two points, xyz graphs. The ones that fit in a \( 2\times n\times n \) grid are just the prisms over even polygons. Up to graph isomorphism there are only three that fit in a \( 3\times 3\times 3 \) grid:
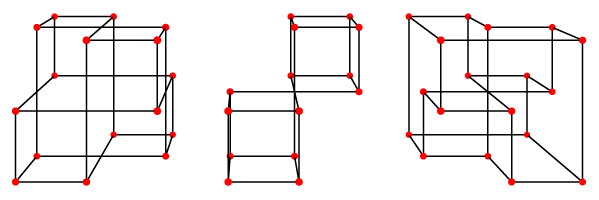
Left to right, the flat polygons of these graphs form a projective plane closely related to the one in the previous posting, a planar graph with nine faces, and a torus with nine hexagonal faces. The enumeration of such graphs within a \( 4\times 4\times 4 \) grid should be well within computational reach since each such graph can be determined by the presence or absence of vertices within a \( 3\times 3\times 3 \) subgrid.
It turns out that a surface formed in this way is orientable if and only if the graph is bipartite. For, if we have colored the vertices black and white, then we can orient the faces in \( xy \)-parallel planes from black to white in the \( x \) direction and from white to black in the \( y \) direction, in \( xz \)-parallel planes from white to black in the x direction and from black to white in the \( z \) direction, and in \( yz \)-parallel planes from black to white in the \( y \) direction and from white to black in the \( z \) direction, forming a consistent orientation of all faces of the graph. Conversely if we orient all faces of the graph, and use the orientation as above to color the faces, the consistency of the orientation will lead to a consistent two-coloring of the graph.
If an xyz graph is connected, it remains connected after removing any one or two vertices, or any one or two edges. For, any path through the removed features can be rerouted the other way around some combination of the flat cycles of the drawing that contain the removed feature. That is, xyz graphs are 3-connected and 3-edge-connected. 3-connected planar graphs are exactly the graphs that form the vertices and edges of convex polyhedra, so every planar xyz-graph comes from a polyhedron in this way; in addition, if the flat faces of an xyz graph form a sphere, they do so in a unique way: one cannot rearrange the graph to cause different cycles to be flat and still have a sphere. Exercise: find a convex polyhedron with the same graph as the middle one shown above.
Any topological surface can be formed by the flat faces of an xyz graph. Method 1: form connected sums of projective planes and tori by connecting them at corners, similarly to the way the planar graph at the center above is formed by connecting two cubes at a corner. Method 2: embed some graph on the surface so that all faces are disks with no repeated vertex or edge in the cycle around any face, and with no edges connecting any vertex to itself. Form the GEM representation of this embedding: a new graph with one vertex per vertex-edge-face incidence of the embedded graph, and with two of these new vertices connected by an edge whenever their triples of features differ in exactly one feature. (See e.g. this paper or better yet the Bonnington-Little book it cites for more discussion of GEM representations.) Choose distinct index numbers for the vertices of the embedding, the edges of the embedding, and the faces of the embedding, and place the GEM vertex corresponding to the incidence between vertex \( i \), edge \( j \), and face \( k \) at the point \( (i,j,k) \), forming an xyz graph. Thus, every GEM is an xyz graph, in which the flat faces of the xyz graph correspond to the features of the original embedding. The resulting xyz graph has the same topology of the starting surface. For instance, the cube can be viewed as the GEM for a digon embedded on a sphere, while the permutohedron can be viewed as the GEM for a tetrahedron. However none of the three 3\times 3\times 3 xyz graphs are GEMs.
ETA: Finally, the size of a cube needed to represent a genus-g surface grows only as the square root of \( g \). For, the xyz graphs formed by the points in an \( n\times n\times n \) grid satisfying \( x+y+z \in \{0,1\} \pmod{n} \) have \( 2n^2 \) vertices, \( 3n^2 \) edges, and only \( 3n \) faces, forming bipartite surfaces with genus \( \Theta(n^2) \). To form genuses other than the ones achievable by this construction in similarly small volume, or nonorientable surfaces with high genus, again use the connected sum operation.