A projective plane in a 3d grid
Suppose we have a point set S in 3d such that any line parallel to a coordinate axis intersects S in either zero or two points. If we draw a graph by connecting pairs of points on the same line, we get a 3-regular graph, such as the one below.
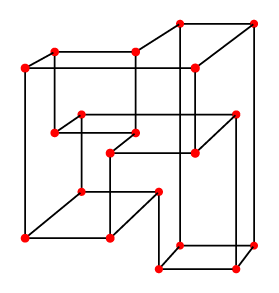
What other properties must such a graph have? For instance, they can't contain a \( K_{2,3} \) subgraph, a triangle, or a pentagon. After thinking some more about the inverse permutohedron example I posted the other day, I started to wonder, do such graphs always form partial cubes?
Sadly, no. The one shown above isn't even bipartite.
If you consider the edges in only two of the three directions in such a drawing, they fall into a collection of (possibly self-crossing) cycles. If we form a surface for each cycle, and glue these surfaces together along any edges they share, we get a manifold, a boundaryless 2d surface. In the case of the inverse permutohedron, this manifold has the same structure as the convex polyhedron we started with: it's topologically equivalent to a sphere even though it's embedded in the 3d grid in a very non-sphere-like way. Every face of the manifold has an even number of sides, and for a sphere that's enough to imply that the overall graph is bipartite. But the graph shown above can't form a sphere because of its nonbipartiteness. It has 20 vertices, 30 edges, and 11 faces; therefore by Euler's formula it's a projective plane.
Incidentally, my students have convinced me to try using Pyx, a package for making postscript or pdf figures using Python, and the figure above was generated using it. Pyx doesn't have 3d perspective built in, so I wrote that part myself; source code for the figure is here.