Simplicial pseudoline arrangements

I just returned from Ireland; I enjoyed my stay greatly and was sad to leave. Photos to come some time later after I've had time to run them all through Photoshop.

I haven't forgotten about simplicial arrangements while I've been gone. Here's something that looks a lot like another one:

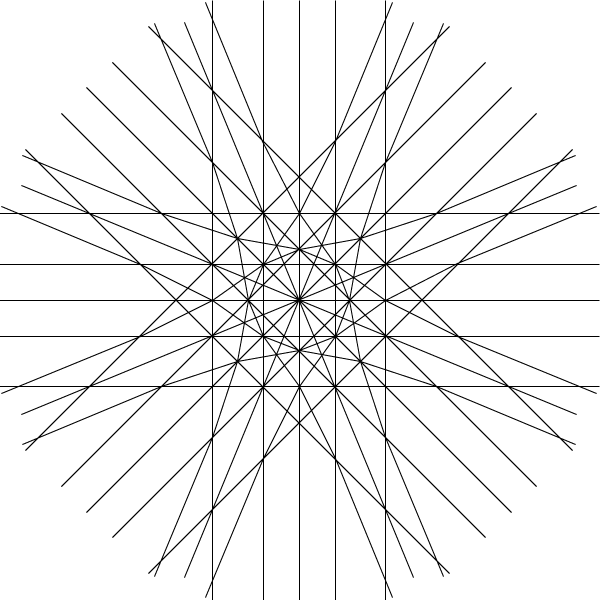
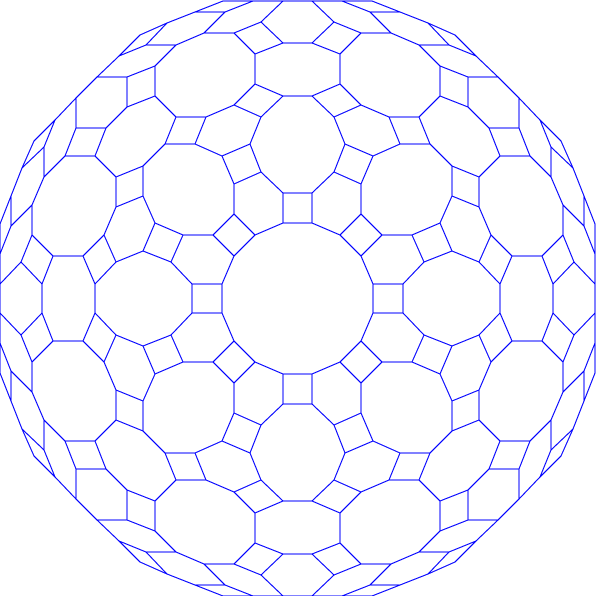
This (together with the line at infinity) is called a simplicial pseudoline arrangement, because the curves in it behave combinatorially like lines (each one topologically equivalent to a line, and each two crossing at a single point in the projective plane, counting parallel lines as crossing at infinity). This arrangement is called non-stretchable, because it's not possible to stretch all the pseudolines in it into actual lines while preserving the pattern of intersections they form; this can be proven by contradiction, using an affine transformation to force the horizontal and vertical lines of the drawing to form a symmetric 4x4 grid of rectangles, and then noting that the symmetries of this grid do not allow some of the other curves that pass through the grid vertices to be straight. Simplicial pseudoline arrangements work as well as lines do for drawing tilings of convex polygons by centrally symmetric tiles (in fact such tilings are one of many equivalent ways known for defining pseudoline arrangements) as well as (via the theory of spreads) for defining cubic partial cubes. Here's the convex polygon tiling corresponding to the arrangement above:

While I was away, my copy of Grünbaum's 1972 book, Arrangements and Spreads, arrived, and it tells me much more. Along with the three known infinite families of simplicial line arrangements, there are (or were in 1972) seven more known families of simplicial pseudoline arrangements, together with additional sporadic examples. Several such arrangements, although not the one above, are illustrated in the figures of the book. So now we've gone from one infinite family of cubic partial cubes and 15 sporadic examples, to ten infinite families and a hundred or so sporadic examples. At this point it seems easiest to explicitly list only the cubic partial cubes that don't come from arrangements, and depend on the arrangement literature for the rest. I should look up the details of these pseudoline families (they're only described vaguely in terms of the number of lines and a few example figures by Grünbaum) because it would be interesting to determine whether the gluing operation for combining different arrangements to form non-arrangement cubic partial cubes also produces infinitely many different results; it doesn't seem to work on the known infinite simplicial line arrangement families.

Comments: