Simplicial arrangements with few slopes
One last post on simplicial arrangements before I leave for Graph Drawing, in Limerick, Ireland (my first trip to that country).
The drawing technique from my previous post (borrowed from my paper on drawing partial cubes) transforms any line arrangement with \( k \) slopes into a tiling of a \( k \)-gon with integer side lengths by smaller unit-side-length centrally-symmetric convex polygons. Although the slopes of the lines may be important for realizability of the arrangement, they do not matter for the \( k \)-gon tiling, so we can assume the outer \( k \)-gon has sides that are parallel to a regular \( k \)-gon. The requirement that the arrangement be simplicial puts additional strong constraints on this tiling: exactly three tiles must meet at each interior vertex, and the boundary vertices may either be part of a single tile or must be the meeting point of only two tiles (with some further conditions depending on whether or not the arrangement includes the line at infinity).
These constraints are so strong that, for small values of \( k \), we can do the case analysis to find all simplicial arrangements with \( k \) slopes. When \( k=2 \), we are looking for a packing of a unit-sided rectangle by squares. In order to avoid degree four internal vertices, we can only pack a single row of squares next to each other. When there is a single square, we must also include the line at infinity, forming a near-pencil with three lines. When there are two or more squares, we may exclude the line at infinity (a near-pencil with one more line than squares) or include it (a near-pencil with two more lines than squares). These rectangle tilings can be thought of as a side-on view of a prism, with the top and bottom of the prism perpendicular to the angle of view; if the line at infinity is included, left and right sides of the prism are also perpendicular to the view.
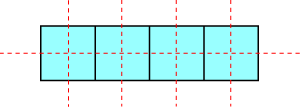
For \( k=3 \) (that is, arrangements with lines of three slopes), we must find a tiling of an integer side length hexagon by regular unit hexagons and 60-120 rhombi. Two such tilings lead to simplicial arrangements without the line at infinity; they are just the near-pencils on three and four lines again. It is not a coincidence that these resemble axonometric drawings of a cube and hexagonal prism respectively.
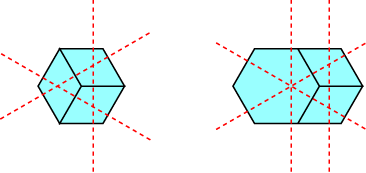
Five more tilings lead to simplicial arrangements with the line at infinity. The first of these is the near-pencil on four lines yet again, but the others do not belong to any of the known infinite families of simplicial arrangements.
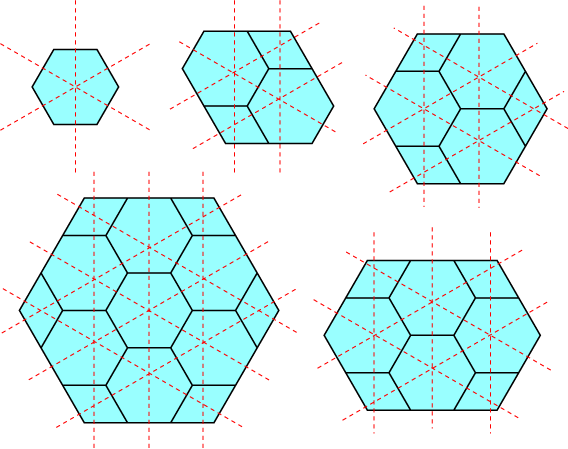
There is one more possible hexagon-rhomb tiling, with a hexagon in the center together with two pairs of rhombs, one on the left side of the hexagon and one on the right, but this does not form a simplicial arrangement; with or without the line at infinity, the infinite faces on the left and right sides of the dual arrangement form one or two quadrilaterals.
More generally, the tilings for simplicial arrangements with \( k \) slopes fill a \( k \)-gon with side lengths at most equal to \( 2k-3 \); for, along any side of the filled \( k \)-gon, the edges of the tiling incident to that side must meet the side one at a time, in slope order, no three consecutive edges having the same slope. Therefore, for any finite \( k \), the number of simplicial arrangements with \( k \) slopes is also finite.