Zonohedra and cubic partial cubes

I just found this paper: Cubic inflation, mirror graphs, regular maps, and partial cubes, by Brešar, Klavžar, Lipovec, and Mohar. According to it, not much is known about the problem of listing partial cubes in which all vertices have exactly three neighbors — there is one known infinite family (the prisms) and several other sporadic examples, among which is the permutohedron (truncated octahedron). The paper defines an expansion operation for graphs on surfaces (essentially the same as the gem representation from topological graph theory) which, when applied to certain planar graphs, leads to a few more examples.

This immediately made me think about zonohedra, since the truncated octahedron is one. Also, any zonohedron has a skeleton that's dual to a central plane arrangement in three-dimensional space (the arrangement of planes through the origin that are perpendicular to the edges of the zonohedron) and, as with the dual of any affine hyperplane arrangement, it's automatically a partial cube. So I thought I'd go through my catalog of interesting symmetric zonohedra to see whether any of them lead to additional cubic partial cubes.

The cube and prisms are examples of the paper's inflation operation applied to even-length cycles of four or more vertices.

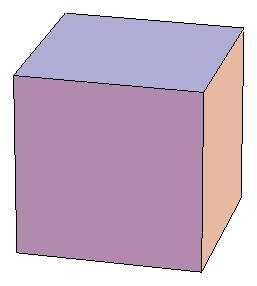
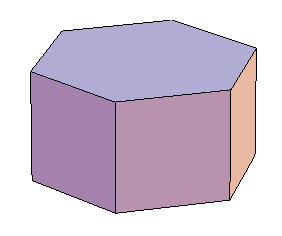
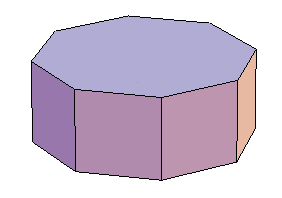
The truncated octahedron is also known as the permutohedron, as its vertices can be given coordinates in 4-dimensional space that are the permutations of the vector (1,2,3,4). It is the example that led me down this line of thought in the first place. It is also an example of the inflation operation, applied to K₄.

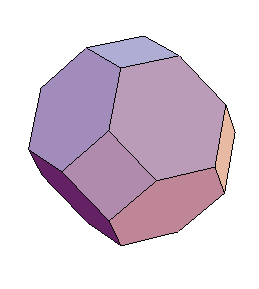
The Great Rhombicuboctahedron is the result of the paper's inflation operation, applied to either the cube or the octahedron (the operation produces the same result on any graph and its dual).

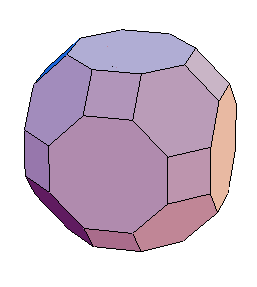
The Truncated Rhombic Dodecahedron is the first example of a cubic zonohedron not resulting from the inflation operation (in inflated graphs, every vertex belongs to a quadrilateral face, while this graph has vertices all of whose adjacent faces are hexagons). It is also not one of the four sporadic cubic partial cubes known prior to this paper, as they had 30, 36, 42, and 48 vertices, while this one has 32. So it must be a new example! Well, sort-of-new, new when viewed as a partial cube, it's been known for a long time in the simplicial line arrangement view of the problem.

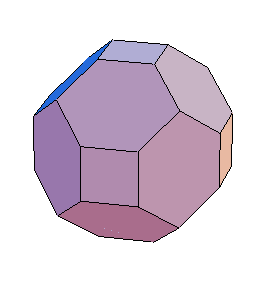
The Truncated Small Rhombicuboctahedron is the result of applying the inflation operation to the Rhombic Dodecahedron, or to the Cuboctahedron (the paper's example in Fig. 3(e)).

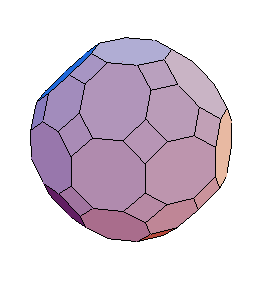
The Great Rhombicosidodecahedron is the result of applying the inflation operation to the Icosahedron or to the Dodecahedron.

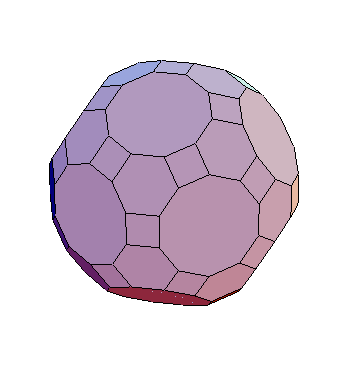
The Truncated Small Rhombicosidodecahedron is the result of applying the inflation operation to the Rhombic Triacontahedron or to the Icosidodecahedron. Another example not listed in the paper.

I seem to recall that a lot more is known about this problem in its dual form. If we view the central plane arrangement dual to a zonohedron as an object in the projective plane (that is, the space having as points the central lines in 3d and as lines the central planes in 3d), then the zonohedron is cubic iff its dual is a simplicial line arrangement; that is, an arrangement of lines in which each face is a triangle. It seems odd that the partial cube people don't know about this connection. A search for that phrase finds statements like, there exist two infinite families of simplicial line arrangements and 91 sporadic examples. I don't know where to find a list of these examples, though; possibly somewhere in Grünbaum's publications. It would also be interesting to find more examples of nonplanar cubic partial cubes.

ETA: After exchanging email with this paper's authors, it appears that the connection between simplicial arrangements and cubic partial cubes was indeed previously unknown. Since it leads to two new infinite families of cubic partial cubes, as well as more sporadic examples, I should probably write it up more formally as a paper. The cubic inflation paper has appeared in Eur. J. Comb. 25 (2004), pp. 55-64, and Klavžar has been working on another paper on the same topic with S. Shpectorov.

---

Comments: