Linkage

Lance Fortnow notices fewer faculty job ads in this year’s November CRA News and asks: “is there a real drop in hiring, or something else?”
Vida Dujmović awarded University of Ottawa Research Chair ($\mathbb{M}$).
POPL 2024 registration is on the order of £2000? It’s convenient that this ridiculous fee is nowhere visible on the POPL web site. This needs to be shown to all the computational geometers who would still like SoCG to return to the ACM fold. (Last year’s early registration fee: $375.)
Characterization of the quadrilaterals that admit billiard circuits ($\mathbb{M}$), Katherine Knox. This means that a billiard ball can bounce once off each side in order before returning to its starting position. The author proved this when she was in 7th grade! See also Geogebra applet.
The corolla ($\mathbb{M}$), something like a crown-shaped 3d flexagon decorated with Escher prints, with making-of blog post.
Mathematical drawing hacks ($\mathbb{M}$), including tips on how to draw Möbius strips, tetrahedra, and curly brackets.
Open access to heritage images is becoming increasingly difficult in Italy ($\mathbb{M}$). The background to this is an Italian court case last year in which The Gallerie dell’Accademia di Venezia, a public museum in Venice, won a lawsuit forcing jigsaw puzzle maker Ravensburger to pay royalties for reproductions of far far out of copyright works by Leonardo Da Vinci. This decision poses a threat not just to toy companies, but to Wikipedia and other users of public domain artworks.
How to plagiarize and get away with it ($\mathbb{M}$, via): become powerful enough that your friends in the court system declare you to be the true author of your bachelor’s thesis and enjoin your university from publishing their investigations. El Pais tells the story of Mexican supreme court justice Yasmín Esquivel.
Robin Houston asks how few adjacent cubes in a $4\times 4\times 4$ grid need to be glued to make the whole thing rigid. I found a solution with 50 glued pairs, the current record, but I’m not convinced its optimal. Image link is a spoiler.
Slide-glide cyclides ($\mathbb{M}$). Banana-shaped pieces (geared at their shared base) that slide past each other to provide a mechanical demonstration of the equality of area of a sphere and a disk of twice the radius. 3d print and video by Henry Segerman.
Why it’s important to choose the right kind of spiral in your designs ($\mathbb{M}$). Bernoulli merely ended up with a permanent mistake on his tombstone (an Archimedean spiral replacing his requested logarithmic spiral). But if you design a rock-climbing cam with a non-logarithmic spiral, or with the wrong logarithmic spiral, its incorrect angle against the rock may fail to protect you from a fall. And spiral wheels with a different carefully chosen shape can be used to design rocking self-propelled skateboards, crutches that help push their users forward, and therapeutic shoes that lengthen the gait of one foot, training people with gait impairments to walk better.
What should I do if I suspect one of the journal reviews I got is Al-generated? ($\mathbb{M}$) Consensus answer: complain to the editor.
The first mathematics publication I know of for the binary tiling or Böröczky tiling of the hyperbolic plane ($\mathbb{M}$) was in 1974 by Károly Böröczky. The same recursive structure appeared earlier, in a 1957 work of M. C. Escher, “Regular Division of the Plane VI”. I thought that might be the beginning of the story, but then I noticed that the Smith chart used in microwave engineering looks very similar: compare the binary tiling (below left) to the Smith chart (right) in the two Wikipedia images below.

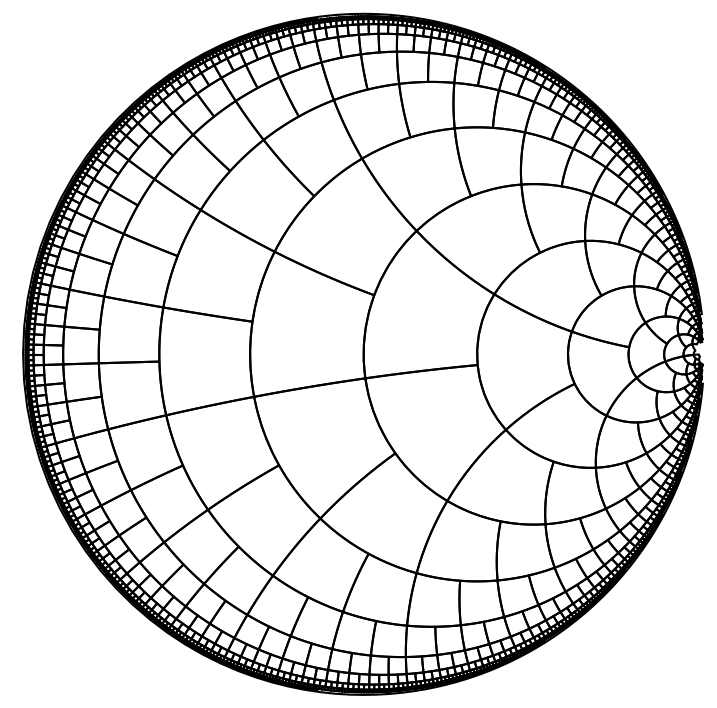
The same subdivision on horocycles and perpendicular hyperbolic lines is present in both images, and the same effect of refining the subdivision like a quadtree as you move further away from the center of the drawing. But the Smith charts perform the subdivision in a more irregular pattern, rather than subdividing at each successive horocycle. The original 1939 Smith chart looks similar, but rotated $90^\circ$ and with an even more irregular pattern of subdivisions. See page 33 of Electronics magazine from January 1939.