The Delaunay complex of a set of points in the Euclidean plane partitions the convex hull of the points into polygonal cells. Each cell is the convex hull of a co-circular subset of the points whose circle does not contain any more points. It’s often called a Delaunay triangulation, because for points in general position the cells are all triangles, but I do not want to assume general position here. It is isohedral when all of the cells are symmetric to each other (maybe a little more strong than asking for them all to have the same shape). For example, the familiar tilings of the plane by squares or regular hexagons are both isohedral and Delaunay. Another example is a tiling of the plane by 60°–90°–120° kites:

Tiling of the plane by 60°–90°–120° kites, with shading showing that the circumcircles of each site are empty of other tiling vertices

Some other tilings, even very symmetric ones, might not be Delaunay. For instance, it is impossible to make a Delaunay version of the Cairo pentagonal tiling because its tiles have two complementary angles or two right angles, impossible for a co-circular pentagon.

In these cases, the symmetries are of the familiar kind, translations and rotations of the plane. But translation symmetry forces us to use infinitely many points. Can finite Delaunay complexes be isohedral? Sort of, maybe, but with a different kind of symmetry. You can translate between Delaunay complexes on the plane and on a sphere by stereographic projection, and translations, rotations, and scaling in the plane become Möbius transformations on the sphere. So the projection onto the sphere of a square grid becomes a spherical Delaunay complex that is symmetric under Möbius transformations.

Stereographic projection of a square grid from the plane to a sphere

Rotations of the sphere are also a very special case of Möbius transformations, so we can look for Delaunay complexes with rotational symmetries. Suppose you have a polyhedron all of whose vertices lie on a sphere, and all of whose faces are symmetric to each other by rotations of the sphere. Then the intersection of the sphere with any face plane of the polyhedron is a circle through the vertices of a face that does not contain any other vertices, the defining property of a Delaunay cell. So these polyhedra are isohedral spherical Delaunay complexes. This is true, for instance, for the Platonic solids and for the two infinite families of bipyramids and the trapezohedra but false for some other isohedral polyhedra like the rhombic dodecahedron and triakis tetrahedron whose vertices cannot all be placed on a sphere.

You can map these spherical Delaunay complexes back onto the plane by stereographic projection again. You might think that the result is always a planar Delaunay complex in which all faces are symmetric to each other under Möbius transformation, but there’s a catch. The projection preserves circles, but it turns inside out the ones that contain the pole of the projection. If they were empty on the sphere, they instead turn into circles in the plane that contain every other point. These inside-out circles correspond to Delaunay cells on the sphere that do not map to Delaunay cells in the plane. For instance, projecting the cube vertices back down to the plane with the pole at the midpoint of a cube edge produces a Delaunay complex with only four quadrilaterals; the other two faces of the cube come from inside-out circles and do not become Delaunay cells.

Delaunay complex of a cube, stereographically projected onto the plane with its pole at an edge midpoint

All of this generalizes directly to 3d Delaunay triangulations, and to isohedral 4d polytopes with cospherical vertices, but less is known about what shapes are possible. The regular 4-polytopes, certainly, have symmetric facets and cospherical vertices, but there are other possibilities as well. The isohedral 4-polytopes with up to 20 sides have been classified, but I don’t know which of these can have cospherical vertices.

There are, at least, three different infinite families of isohedral 4d polytopes with cospherical vertices, analogous to the bipyramids and trapezohedra. To describe this, it helps to think of four-dimensional Euclidean space as having two complex numbers \(\alpha\) and \(\beta\) as coordinates, and the unit sphere as the points for which \(\vert\alpha\vert^2+\vert\beta\vert^2=1\). These are the state vectors of a qubit, so we can write these points on the sphere using quantum notation as \(\alpha\,\vert0\rangle+\beta\,\vert1\rangle\), where \(\vert0\rangle\) and \(\vert1\rangle\) are just the two basis vectors for the two-complex-number coordinate system. In this notation, consider the following three sets of points, all on the unit sphere, for integer parameters \(n\) and \(m\):

  • Let \(X\) be the set of \(n\) points \(e^{2\pi i/n}\,\vert0\rangle\), for the integers \(i\) with \(0\le i\lt n\). These form a regular \(n\)-gon in the plane \(\beta=0\).

  • Let \(Y\) be the set of \(m\) points \(e^{2\pi j/m}\,\vert1\rangle\), for the integers \(j\) with \(0\le j\lt n\). These form a regular \(m\)-gon, in the perpendicular plane \(\alpha=0\).

  • Let \(Z\) be the set of \(mn\) points

    \[\frac{1}{\sqrt 2}e^{2\pi i/n}\,\vert0\rangle + \frac{1}{\sqrt 2}e^{2\pi j/m}\,\vert1\rangle,\]

    for the same ranges of \(i\) and \(j\). These lie on a flat torus, the Cartesian product of two circles, and form the vertices of a tiling of the torus by rectangles.

Then the convex hull of \(X\cup Y\) has as its facets \(mn\) congruent tetrahedra, each formed as the convex hull of an edge of the \(X\)-polygon and an edge of the \(Y\)-polygon. The convex hull of \(Z\) is a duoprism whose facets are two kinds of prisms: the Cartesian product of an edge of the \(X\)-polygon with the whole \(Y\)-polygon, and vice versa. When \(n=m\) these two prisms are congruent and the resulting duoprism is isohedral, and dual to the convex hull of \(X\cup Y\). Here is a stereographic projection for \(n=m=18\), taken from the Jenn 3d website:

Stereographic projection into 3d of a 4-dimensional polytope, the (18,18)-duoprism, appearing as a torus tiled with squares

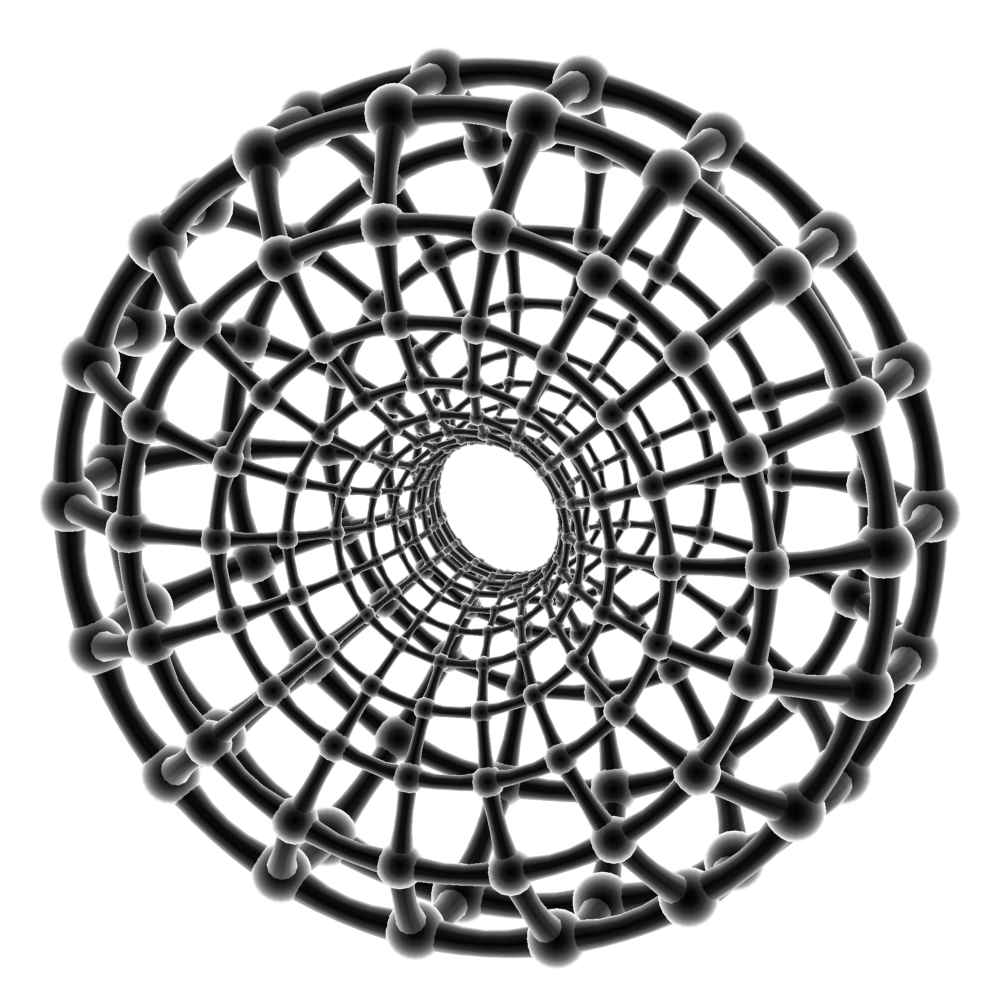
In this image, the most prominent feature is the tiling by squares of the torus containing \(Z\). If you follow sequences of edges of this square grid, through opposite edges at each vertex, you will also see many 18-gons. Some of the 18-gons slice the “inside” of the torus radially into distorted prisms; these are Delaunay cells. Many of the perpendicular 18-gons slice across the “donut hole” of the torus, forming more Delaunay cells. But some of the remaining 18-gons lie on the convex hull of the shape, and cannot be used as slices for the projected set. The missing slices cause the Delaunay triangulation of the stereographic projection to miss some cells, and that can only happen because the spheres for these cells were inverted by the projection.

You can also take the convex hull of \(X\cup Y\cup Z\). This has two triangular-prism facets for each tetrahedron of \(X\cup Y\), meeting at one of the squares of \(Z\). The reason I’m interested in this example comes from my most recent post, on flip-width of geometric graphs. If you take an induced subgraph of this polytope, consisting only of the points in \(X\cup Y\cup Z\) whose coefficients \(i\) and \(j\) are both even, the result is a subdivided complete bipartite graph \(K_{n,n}\), where by “subdivided” I mean that each edge of \(K_{n,n}\) has been replaced by a two-edge path. This isn’t an interchange, in the sense of the previous post, but it has unbounded flip-width, because it is a sparse graph that does not have bounded expansion.

What I really want, though, is a 3d Euclidean Delaunay triangulation with unbounded flip-width, not a non-triangulation complex and not a 4-polytope (I already had one of those in my previous post). To get this, use a stereographic projection whose pole is on the central torus, in the middle of one of the squares (or really on the corresponding point of the unit sphere), and note that the Delaunay spheres of the polytope faces will intersect this torus in Delaunay circles of the squares. But for a square grid, the center of each square belongs only to the circumcircle of that square, not to any of the other circumcircles. So the pole of the projection will only belong to two of the Delaunay spheres, the two sharing the chosen square. The two prisms for these two spheres will be missing from the Delaunay complex (instead, their union, some sort of gyrobifastifium, will form the convex hull of the points), but all the other prisms will still be present. They contain all the edges of the graph, so it still contains a large induced subdivided biclique. Perturbing the points slightly to get a triangulation rather than a complex doesn’t change this.

(Discuss on Mastodon)