Midsphere facts and fallacies
Some three-dimensional convex polyhedra have a midsphere, a sphere tangent to all of their edges. More strongly, every three-dimensional convex polyhedron has a combinatorially equivalent form, called a “canonical polyhedron”, that has a midsphere. The literature on midspheres is a little sparse and missing some key facts and counterexamples, so I thought I would collect some of them here.

The midsphere, when it exists, has a center equidistant from all the edges, and all of the lines through edges. The set of points equidistant from two skew lines is a curved surface, a hyperbolic paraboloid, but when two lines cross each other the set of points equidistant from both lines is instead the union of two planes, perpendicular to each other and to the plane of the crossing lines, through the crossing point of the two lines. For the midsphere of a polyhedron, and two edges incident on a face of the polyhedron, only one of these two planes is relevant, the one that bisects the interior angle of the face. The center of the midsphere (if it exists) can be found at the point where all of these face-angle-bisecting planes meet.
A convenient class of examples of polyhedra with midspheres is given by “Crelle’s tetrahedra”, the tetrahedra with midspheres. For every such tetrahedron, one can find four spheres, centered at the tetrahedron vertices, tangent in pairs at the points where the midsphere touches the edges. The tetrahedron’s six edge lengths are sums of radii of two of these four spheres. Conversely, for every four pairwise-externally-tangent spheres whose centers are not coplanar, the convex hull of the centers is one of Crelle’s tetrahedra. The radii of the four spheres can be varied continuously, keeping them in contact, although not every quadruple of radii works: the Cayley–Menger determinant of the six sums of pairs of radii must be positive. For instance, if three radii are equal and the fourth is much smaller, the three large spheres will be too far apart for the fourth sphere to touch all three of them and the determinant will be negative. Because Crelle’s tetrahedra can be parameterized by four radii, they form a four-dimensional subspace of the six-dimensional space of all tetrahedra (as parameterized by edge lengths).
Some sources either state that the midsphere touches the polyhedron edges at their midpoints, or define a midsphere to be a sphere through all the edge midpoints. But even when a polyhedron has both a midsphere and a sphere through all of its edge midpoints, these two spheres might not be the same as each other. An example is given by the right pyramids over equilateral triangles, parameterized by the quadruples of radii \((1,1,1,x)\) for \(x\ne 1\). These pyramids have an equilateral-triangle base, which both spheres touch at the edge midpoints. But the three edges of length \(1+x\) meeting at the apex of the pyramid are touched by the midsphere at unit distance from the base, rather than at their midpoints.
Anthony Pugh’s 1976 book Polyhedra: A Visual Approach claims that only the Platonic solids have all three of an insphere, midsphere, and circumsphere, but this is not true. Crelle’s tetrahedra are counterexamples. Even with the midpoint-based alternative definition of midspheres, the pyramids are counterexamples.
For a long time the Wikipedia article on midspheres stated that the midsphere gets its name from being between the insphere and circumsphere. But it is not always between them. For a very tall pyramid (with large \(x\)), the circumsphere passes very close to the plane of the equilateral triangle at the base of the pyramid, and the midsphere pokes out past the circumsphere below the base. I briefly thought that the midsphere might be the same as the smallest sphere that touches or contains all of the edges of a polyhedron. In general, even when a midsphere does not exist, this smallest sphere can be found in linear time, as an instance of quasiconvex programming. But for very flat pyramids (\(x\) close to its minimum value), the smallest touching sphere has the incircle of the base as its equator, while the midsphere is larger. The same flat pyramids have an insphere that touches their isosceles-triangle faces at points close to the apex of the pyramid, outside the midsphere, so their insphere pokes out of the midsphere.
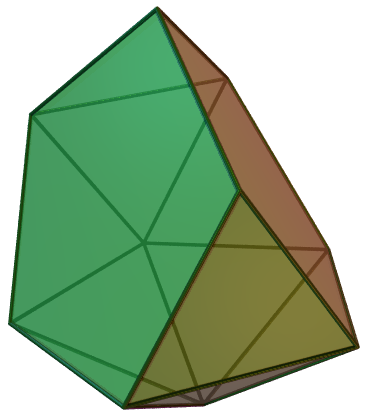
For most polyhedra having an insphere and a midsphere, or a midsphere and a circumsphere, these spheres are not concentric. They are concentric for symmetric polyhedra, such as the Platonic solids, but those are not the only cases. For instance, when a polyhedron with concentric midsphere and circumsphere, like a regular icosahedron, is sliced by the plane through a cycle of its edges, the result continues to have the same concentric midsphere and circumsphere. The metabidiminished icosahedron below is an example. The polar dual of a polyhedron with concentric midsphere and circumsphere instead has concentric insphere and midsphere.
It may possibly be the case that the inradius is always less than the midradius (when both exist) and that the midradius is always less than the circumradius (when both exist). I don’t have a proof, but I also don’t have a counterexample.