Linkage

Neil Sloane has a new blog ($\mathbb{M}$), subtitled “interesting sequences I need help with”. His first post concerns the two-up sequence, formed in steps where the $k$ th step adds two numbers that are not already in the sequence and are relatively prime to the preceding $k$ . Most of the terms appear to be the primes (in order). The remaining terms appear to be prime powers or semiprimes but this has not been proven.
Schwarz lantern ($\mathbb{M}$), a polyhedral cylindrical surface that you can fold from paper. As you make its triangles smaller relative to the cylinder size, it approximates the cylinder in distance, but not necessarily in surface area. This example became one of the original motivations for research on non-obtuse mesh generation algorithms, because its non-convergence to the correct area happens when its triangles are very obtuse. Now a Good Article on Wikipedia.
The graph of ancestors ($\mathbb{M}$). For Father’s Day, Ken Regan tries to find a more principled way of quantifying pedigree collapse (the unavoidable existence of inbreeding among one’s ancestors) than “implex”, the difference between $2^k$ and the number of distinct $k$-step ancestors.
John Baez describes the work of Hoàng Xuân Sính (see also), a student of Grothendieck who became the first female mathematician in Vietnam.
Accepted papers to the 34th Canadian Conference on Computational Geometry ($\mathbb{M}$), to be held in August in Toronto. For mine, see recent blog posts on Dehn rank, octagonal reflections, and flattening paper surfaces. In other news, from looking at the web site, I see that the host university, formerly Ryerson, has changed its name: now it’s Toronto Metropolitan University.
Tetration in busy-beaver Turing machines and in Conway’s Game of Life ($\mathbb{M}$, see also).
Paper show ($\mathbb{M}$): Group art exhibit featuring 14 different artists who work in papercraft. Coming soon to a gallery in the Mission in San Francisco. Maybe the most geometric are the paper geodes of Huntz Liu.
Two 3-regular penny graphs ($\mathbb{M}$). You can’t make these avoid triangles altogether (see my paper on triangle-free penny graphs) but the larger one of these two avoids pairs of triangles that share an edge. It’s more difficult than it seems like it should be to get all of the pennies that should be touching to actually touch, and I didn’t entirely succeed, but I think the pattern is clear.
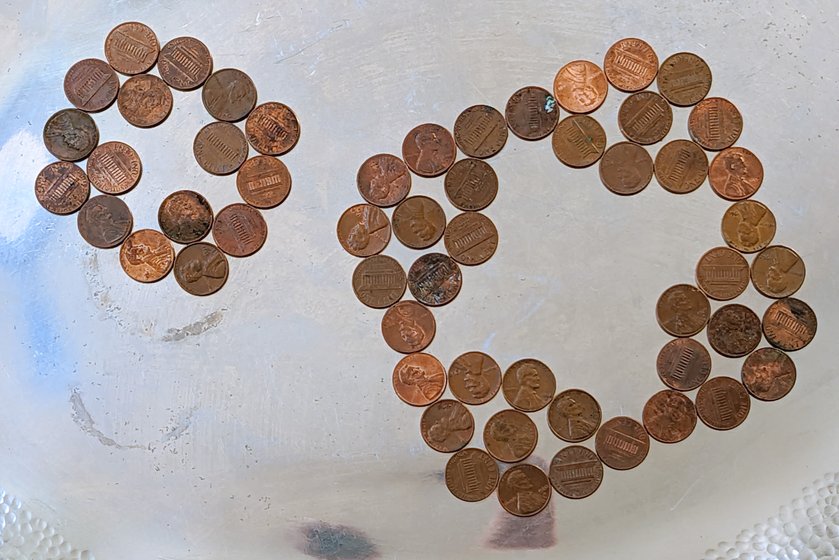
The double bubble theorem ($\mathbb{M}$) states that the minimum area enclosing two volumes looks like a double soap bubble, with three spherical patches meeting at $120^\circ$ angles on a circle. Just after getting Wikipedia’s article to Good Article, I learned of significant progress: Milman and Neeman announced a proof of the triple bubble conjecture in all dimensions and related results. See their preprint or Frank Morgan’s review.
An elaborate hoax history of medieval Russian history is uncovered on the Chinese-language Wikipedia ($\mathbb{M}$, via, mf). Link goes to Chinese state media, but is in English; see also the English Wikipedia internal report on the situation.
Geometrikum ($\mathbb{M}$): geometric exhibits at the Institute for Applied Geometry of the University of Linz. Or, if you’re not near Linz, you can see them online. Includes string-art surfaces, Lego Stanford bunny and trefoil knot, some regular 4-polytope skeletons, papercraft polycubes and modular polyhedra, matchstick tetrastix, and more.