Linkage

What is a natural question? (\(\mathbb{M}\)) Gasarch on distinguishing notions of interestingness of mathematical problems based on ability to answer them, versus whether they lead to deeper mathematics.

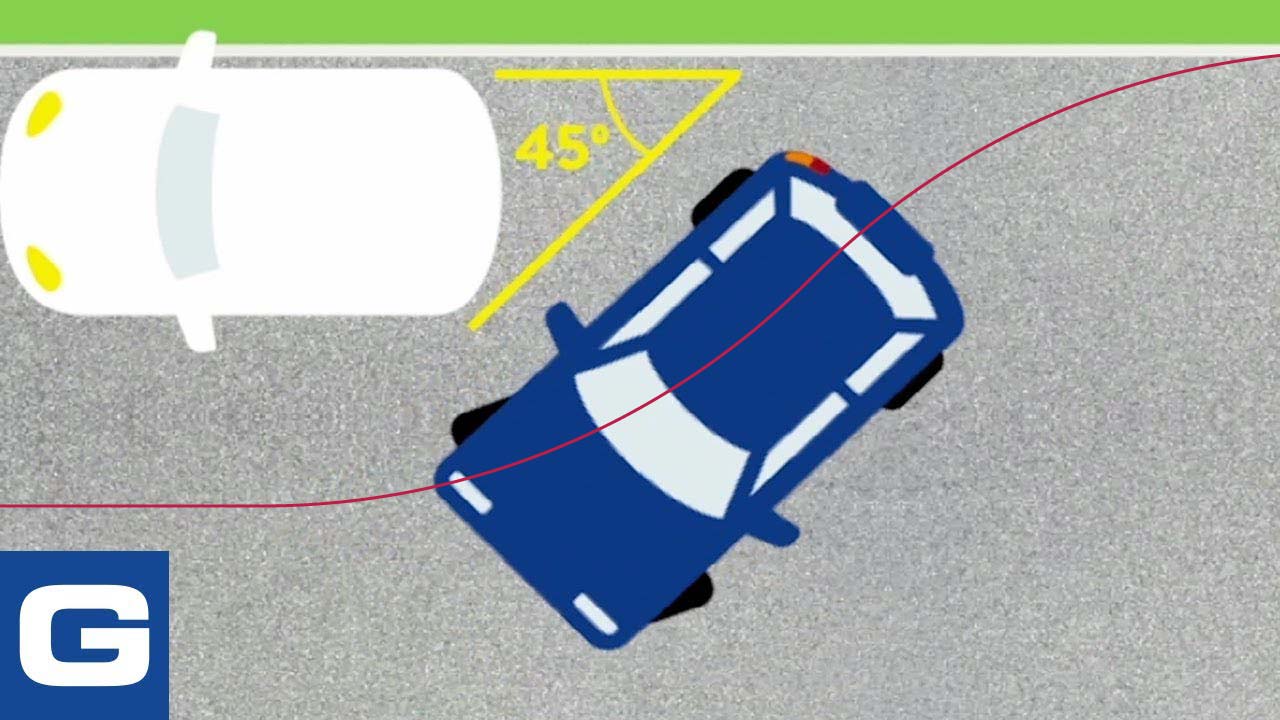
Bad geometry in an illustration of parallel parking advice to change steering lock-to-lock when you reach a 45° angle (\(\mathbb{M}\)): this car is going to end up halfway over the curb. Really the inflection angle depends on the distance from curb and your car’s turning radius. You should switch direction when the rear axle midpoint is halfway between its starting and ending lines of motion, or approximately when the passenger rear wheel is a bit less than halfway to the curb. This car went past that point and can’t straighten before reaching the curb.

How smooth can Nash–Kuiper embeddings be? (\(\mathbb{M}\)) Recent progress identifies a strict threshold at \(C^{1,1/2}\). A new popularized and high-level survey on Quanta. See Wikipedia for more on the Nash embedding theorem (here, in the form that all 2d surfaces have non-smooth embeddings in 3d preserving distances along surface curves) and on the notions of fractional smoothness considered here, left unexplained by the Quanta article.

Interesting progress report by Peter Scholze on the formalized and computer-verified proof of some difficult material in analytic geometry (\(\mathbb{M}\)).

A mathematical foundation for foundation paper pieceable quilts (\(\mathbb{M}\), via). They formalize things by hypergraphs, but I prefer antimatroids: a pattern is piecable if and only if you can slice off one piece at a time by guillotine cuts, eventually slicing everything. The possible slicing orders form an antimatroid, because a piece, once sliceable, remains so until it is sliced. The piecing order is the reverse of a slicing order.

Firefox’s “reader mode”, in which you can click on little page-with-text icon next to the url, and get view of text stripped of extraneous framing, is useful (\(\mathbb{M}\)), but it would be more useful if it actually worked for pages with mathematical content.

One of the footpaths through my neighborhood is next to a small field with two chess tables (\(\mathbb{M}\)). They’ve been overgrown and largely unused for quite a while, but a few months back the neighborhood association’s gardeners cleared the field and planted some ginkgo trees around the tables. Someone has been playing chess there with pine cones:

Scott Aaronson, in Quanta, on why the glib popularizations of quantum computing typically found in publications like Quanta are usually wrong (\(\mathbb{M}\), see also).

The amazing, autotuning sandpile (\(\mathbb{M}\)). Jordan Ellenberg on abelian sandpile models, with pretty pictures of the fractal patterns they generate, from 2015. These patterns are still a topic of active research; see e.g. “The Apollonian structure of integer superharmonic matrices”, Ann. Math. 2017, , and “Harmonic dynamics of the abelian sandpile”, PNAS 2019.

Dodecahedral trajectory (\(\mathbb{M}\)). Mathematical glass artist Bronna Butler visualizes closed geodesics from and returning to a single vertex on the dodecahedron, using stained glass. These paths exist only on the dodecahedron, among the Platonic solids: geodesics starting from a vertex on the other solids will either hit another vertex before returning, or never return.

Automatic face-recognition systems used to auto-crop social media photos discovered to be racist and sexist (\(\mathbb{M}\)). This sort of thing is part of a long line of stories of computer systems learning to replicate the biases of their developers, and one of many reasons we need greater diversity in CS.

Introduction to Computational Origami (\(\mathbb{M}\)), Ryuhei Uehara’s 2020 book, is the subject of a new featured review by Tom Hull on MAA Reviews.

Howell’s moving orbits (\(\mathbb{M}\)). Greg Egan explains the early research of Kathleen Howell on the existence of first-order-stable halo orbits of a third small body under the gravitational influence of two larger bodies, related to the (unstable) L1 and L2 Lagrange points.

The 2021 Bridges Conference Mathematical Art Galleries (\(\mathbb{M}\)) are online even though the online conference itself is not until August. I haven’t yet had time to explore all of them but there are lots of good pieces in there.