Forced creases in Miura folding

I've posted before about the Miura fold, a subdivision of a sheet of paper into paralellograms that gives a nice smooth motion from a compact folded state (in which the parallelograms are all folded on top of each other) to an unfolded state in which the paper is nearly flat. But this pattern can have defects that interfere with its folding pattern, in which small subunits of the pattern fold the wrong way: they still have the same creases but some of them are backwards. My latest arXiv preprint, "Minimum Forcing Sets for Miura Folding Patterns" (arXiv:1410.2231, with Ballinger, Damian, Flatland, Ginepro, and Hull, to appear at SODA) studies the number of creases that need to be forced to go the right way, in order to be sure of getting the correct Miura fold for the rest of the creases as well.

One of the key ideas in the paper comes from some previous work by undergraduate co-author Jessica Ginepro with her advisor Tom Hull (tomster0). They showed that the different ways of folding the Miura pattern (the right way, and the many wrong ways) have a one-to-one correspondence with the different ways of properly 3-coloring a grid graph. The correspondence uses a non-obvious boustrophedon pattern of sweeping the grid in alternating order, left to right, right to left, left to right, etc., using the differences between consecutive colors in the sweep to determine the direction to fold each crease.

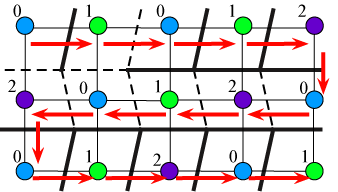
Under this correspondence, a forcing set of creases in a Miura pattern becomes a forcing set of edges in the grid, such that if you label each selected edge with the difference (mod 3) of the colors of its endpoints, no other valid coloring has the same pattern of differences.

Based on this correspondence, and some other combinatorial tools including domino tiling and planar feedback arc sets, we can show that the standard Miura folding pattern is the worst Miura, in the sense that it requires a bigger number of forced creases (approximately half of the creases) than any other way of folding the same pattern. In terms of the corresponding grid coloring, the Miura pattern forms a checkerboard of two colors, and any one of its grid squares can be recolored in a different color unless it has a forced edge incident to it, so there have to be a lot of forced edges.

In constrast, some other folding patterns for the same crease set can be forced by much smaller subsets of creases, proportional only to the square root of the total number of creases. For instance, fold a sheet of paper into a strip, folding each crease the same way so that the paper spirals around itself:

Then fold the strip in a spiral around itself again, so that the second set of folds are all parallel to each other but tilted a little rather than being perpendicular to the first set of folds:

This corresponds to a nice regular pattern of three colors in the grid in diagonal stripes, which is much more highly determined: if you fix the colors on the boundary of the grid, everything inside has its color forced. So, it has much smaller forcing sets (in fact, the smallest possible among all wrong ways of folding the Miura).

More generally, for any pattern of folding the Miura (right or wrong), we can construct a minimum subset of the pattern that forces the rest, in polynomial time.

Comments: