Several important families of objects in combinatorics and order theory can be represented as collections of dichotomies (partitions of a set into two subsets), where each pair of dichotomies in the collection must be compatible with each other. Examples, described in more detail below, are the family of weak orders on a fixed set of objects, the family of trees on a fixed set of leaves, the family of plane trees on a set of leaves with a fixed cyclic order, the family of set partitions, the family of partitions of a convex polygon by its diagonals, and the family of subsequences of a linear order or cyclic order. When this happens, we can form a graph linking compatible pairs of dichotomies, and represent the objects in question as cliques in this compatibility graph. Cliques form a median algebra: if any three cliques vote on which vertices to include or exclude, the result is again a clique. This means that the same sort of median structure can be extended to other objects such as weak orders and trees. More, we can use ideas such as the clique complex and simplex graph to form topological spaces and graphs that represent these families of objects.

Weak orders

A weak order of a set of items is just a linear ordering with ties. It can be represented geometrically by assigning a real number to each item and using the comparisons of the numbers, but it can also be represented as a set of ordered dichotomies specifying that some subset of the items comes before all the other items. There are \( 2^n-2 \) possible ordered dichotomies (one for each nontrivial subset of the items) and two of these dichotomies are compatible if the set that comes first for one of them is a subset of the set that comes first for the other or vice versa.

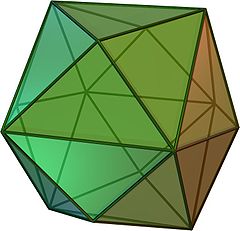
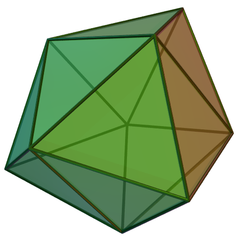
The compatibility graph of dichotomies on three items is just a 6-cycle, but for four items it is a tetrakis hexahedron. More generally for any number of items it is the dual polytope to a permutohedron. Thus, in the picture below, every vertex, edge, and triangle represents a weak order on four items, as does the empty set (representing the weak order in which everything is tied). In a weak order represented by a vertex, either there are two pairs of tied items (the six octahedron vertices) or one group of three tied items (the eight cube vertices). The weak orders represented by an edge have one pair of tied items, and the weak orders represented by a triangle are actually total orders.

The tetrakis hexahedron, representing the weak orders on four items

There is an alternative way of describing the same graphs: in a hypercube (representing the family of all subsets of an \( n \)-item set), add an edge from any set to any of its supersets. Geometrically, these edges correspond to the partition of the hypercube into orthoschemes. Now remove the vertices corresponding the empty set and the whole set, to get the comparability graph forming the weak orders. Thus, the six-cycle is formed by removing two vertices from a triangulated cube (below), and the tetrakis cube is formed by removing two vertices from a triangulated hypercube.

A triangulated cube, with two opposite vertices whose removal leaves a 6-cycle

Trees

Each edge in a tree defines an unordered dichotomy: a partition of the leaves into two subsets (the two subtrees formed by deleting the edge) with no preference for one subtree over the other. The leaf edges are not an interesting part of the compatibility graph, though, because the splits they form are present in all trees, so we only consider the dichotomies with more than one element on each side. Two of these dichotomies are compatible if they do not cross: one of the four intersections of a subset from one dichotomy and a subset from the other is empty. The compatibiliy graph dichotomies on five items is just the Petersen graph.

The Petersen graph

The compatibility graph of dichotomies on six items is a 25-vertex graph that I have had some difficulty drawing. The 2-4 dichotomies have neighborhoods that look like tetrahedra with subdivided edges, but the 3-3 dichotomies have neighborhoods in the form of the graph \( K_{3,3} \) whose most natural geometric representation is four-dimensional. There's some resemblance to the tetrakis cube above: like the 2-2 weak orders, the 3-3 dichotomies form an independent set, while like the 1-3 weak orders, The 2-4 dichotomies form a subgraph with something resembling a cubical structure: it resembles a quotient of an infinite 3d grid, formed by a 3x3 cube with opposite ends glued with a twist, but that has the wrong number of vertices and it seems difficult to fit the 3-3 dichotomies into this view.

Plane trees and polygonal partitions

If a regular \( n \)-gon is partitioned into smaller polygons by adding some of its diagonals, the planar dual graph to the resulting map is essentially the same as a tree, embedded in a noncrossing way in the plane, with its leaves placed in cyclic order on the midpoints of the polygon edges. So polygonal partitions and plane trees on a set of cyclically ordered leaves can be thought of as essentially the same thing. We can also choose one of the polygon edges to be the root and get an equivalence to rooted trees on a set of linearly ordered leaves, described e.g. here. Since it makes for prettier pictures, I tend to prefer the polygonal partition interpretation.

Each diagonal of the polygon can be thought of as a dichotomy, splitting two sets of polygon edges. Two diagonals are compatible when they do not cross each other. The compatibility graph of diagonals of a pentagon is just itself a five-cycle, but the diagonals of a hexagon form a prettier graph, the triaugmented triangular prism formed by gluing pyramids onto the square faces of a triangular prism. More generally, the diagonals of an \( n \)-gon have a compatibility graph dual to an associahedron. Thus, the empty set and each vertex, edge, or triangle of the graph below represents a partition of the hexagon by a compatible set of diagonals, a plane tree on six cyclically-ordered leaves, or a rooted plane tree on five linearly-ordered leaves.

The triaugmented triangular prism, representing polygonal partitions of a hexagon

Set partitions

A partition of a set of \( n \) items into smaller sets may be represented as a family of ordered dichotomies, where each dichotomy separates two or more of the items from the rest of the items. The singleton sets of the partition cover all remaining items not separated out in this way. Thus, there are \( 2^n-n-1 \) possible dichotomies, one for each set of two or more items, almost the same family of dichotomies as the one forming the weak orders. However the compatibility relation is different: two of these ordered dichotomies are compatible if the sets they separate out are disjoint.

The compatibility graph one gets in this way is kind of messy, though. E.g., for five items, it has six isolated vertices (one for each of the six four- and five-item sets), a Petersen subgraph (for the vertices representing two-item sets), and ten degree-one vertices connected to each of the Petersen vertices (representing three-item sets). So the big connected component is, completely by coincidence, the same as the one I used a few days ago to depict an NP-completeness reduction for finding Christmas cacti:

Graph formed by adding a new leaf neighbor to each vertex of the Petersen graph

Subsequences and subpolygons

The subsequences of an \( n \)-item linear or cyclic sequence may be specified by a binary variable per item, describing whether it's in or out, but that doesn't lead to a very interesting compatibility graph (it's just an \( n \)-vertex complete graph) and it doesn't say very much about the sequence ordering. Instead, one can represent a subsequence by a collection of dichotomies representing maximal contiguous subsequences of omitted items. I think this representation is clearer for the cyclic sequence case, in which the whole sequence can be thought of as the vertices of a regular \( n \)-gon and any subsequence (at least, of three or more items) can be thought of as a convex polygon formed by some of the vertices of the whole sequence. A dichotomy (at least, the ones that omit fewer than  \( n-1 \) items) can be thought of as a diagonal of the \( n \)-gon, and the convex polygon formed by a subsequence has as its sides these diagonals together with some of the \( n \)-gon's sides. The compatibility condition on diagonals (no two should exclude the same vertices, nor overlap to form a larger subsequence of excluded vertices) is very similar to that for set partitions, and the compatibility graph for subpolygons also resembles that for partitions. For instance, for subsequences of a 5-item cyclic sequence (subpolygons of a regular pentagon) there are six isolated vertices (the dichotomies that exclude four or five items of the sequence), five vertices with a single neighbor (the dichotomies that exclude three items), and five vertices forming a pentagon (the dichotomies that exclude two items). In the case of a 6-item cyclic sequence, the compatibility graph is as drawn below, together with a degree-one vertex attached to each of the degree-five vertices shown below and a set of seven isolated vertices.

Compatibilty graph of a 6-item cyclic sequence

If the subsequence must have three or more vertices (so that it forms a subpolygon) a closely related graph on a subset of these vertices with a stronger compatibility relation works.

I was hoping to find some other nice triangulated graphs in this way, such as the Shrikhande graph, but I didn't find clean combinatorial interpretations for its cliques.