Symmetric embeddings of cubic symmetric graphs
A cubic symmetric graph is a graph in which every vertex has exactly three neighbors, and in which there are symmetries taking every vertex to every other vertex and every edge to every other edge; a catalog of these graphs, up to 768 vertices, can be found in the “Foster census.”
Each row of the adjacency matrix of a cubic symmetric graph can be interpreted as a vector of 0-1 coordinates for the vertex corresponding to that row. This interpretation embeds the graph onto a \( (n-1) \)-dimensional hypersphere, the intersection of the sphere of radius \( \sqrt{3} \) centered at the origin with the hyperplane \( \sum x_i=3 \). Every symmetry of the graph is preserved as a symmetry of the embedding, but the dimension is too large for this to be useful in visualization. In some cases we can get a much lower dimensional embedding that still preserves all the symmetries, or at least enough of them to be sure that the graph is symmetric.
Two dimensions is too small for anything interesting to happen, but here are three examples in 3d. The complete graph \( K_4 \), when embedded using its adjacency matrix, turns into the skeleton of a regular tetrahedron (drawn below with curved edges on a sphere). But the regular cube and regular dodecahedron also have three-dimensional symmetric embeddings despite having larger numbers of vertices.
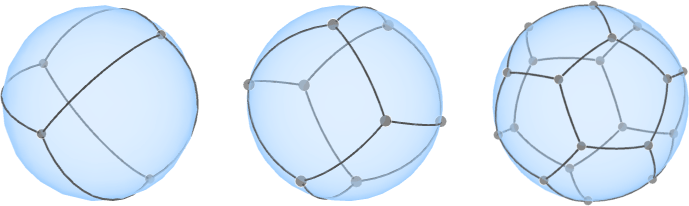
Figures produced using Jenn
There are two more especially nice examples in four dimensions. Draw the pentatope as a regular subdivision of the unit sphere in four dimensions into spherical tetrahedra, place a vertex at the midpoint of each edge and at the centroid of each triangle of this subdivision, and place a great-circle edge connecting every edge midpoint with every centroid of an adjacent triangle. The result is a symmetric embedding of the Desargues graph in which every vertex has three edges meeting at 120-degree angles. The same edge-triangle placement also works starting from the 24-cell to produce a nice embedding of a 192-vertex cubic symmetric graph.
The square flat torus can be embedded onto a hypersphere in 4d as the solution to the equations \( x^2+y^2=1 \) and \( w^2+z^2=1 \), but the graphs embeddable in a symmetric way onto the square torus all have four edges per vertex. I'm not so sure about the hexagonal torus. If it also has a symmetry-preserving embedding onto the unit sphere in 4d, then an infinite family of cubic symmetric graphs formed by cutting and gluing part of the hexagonal tiling of the plane would have four-dimensional symmetric sphere embeddings. The hexagonal torus does at least embed nicely into a hypersphere in six dimensions with the coordinates \[ \bigl(\sin\theta, \cos\theta, \sin\varphi, \cos\varphi, \sin(\theta+\varphi), \cos(\theta+\varphi)\bigr), \] providing six-dimensional symmetric embeddings for this infinite family of graphs.
ETA: The line graph of the Desargues graph also has a nice embedding of this type.