Sudoku triple threat bug
I finally tracked down the "triple threat in bilocal analysis" bug that was occasionally biting my Sudoku program. More for my own benefit than because I think anyone else might care, here's the explanation.
The analysis in question involves drawing a graph, the edges of which connect puzzle cells that are the only two cells in their row, column, or block to contain a specific digit. We then look for cycles in which no two consecutive edges are labeled by the same digit; in such a cycle each cell can contain only the two digits labeling the adjacent cycle edges. The way my algorithm implements this is to perform strong connectivity analysis in a related directed graph, from which we can test which edges belong to nonrepetitive cycles. If a cell has edges with two different labels belonging to nonrepetitive cycles, we know that we can eliminate all other digits as possible values for that cell.
But what happens when a cell has edges with three or more different labels, all belonging to nonrepetitive cycles? Which two digits should we restrict the cell's values to? I used to think that this situation could not arise in a valid Sudoku puzzle, so my code raised an exception in this case. That was the bug. It can happen. Consider for instance the following puzzle:
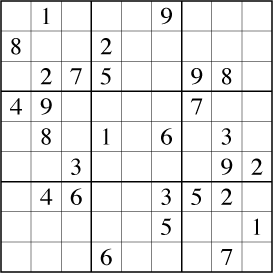
After some earlier steps (including a previous pass of the same sort of bilocal analysis) we reach the following configuration:
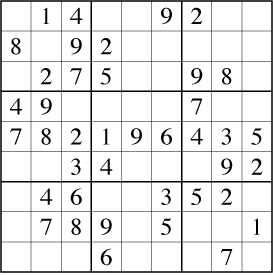
Two different cycles are possible here, both sharing the same edges for part of the cycle and diverging for another part:
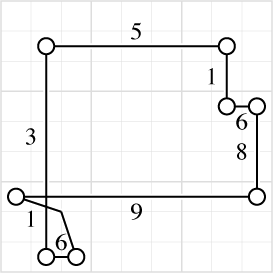
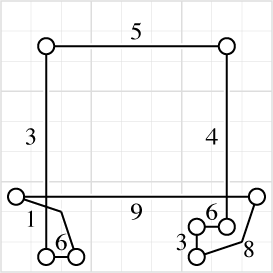
Note especially cell R2C8, in the top right corner. One cycle uses edges labeled 1 and 5 at that cell; the other cycle uses edges labeled 4 and 5. So this is an example of the triple threat that I raised an exception for. But it's still a valid puzzle: if we restrict R2C8 to contain only 4 and 5, and to contain only 1 and 5, it still has a possible value, 5. The two cycles together allow us to make a stronger deduction than if we had only one of them. If there were a third cycle, labeled with 1 and 4, then we would truly have a contradiction, but no such cycle exists.
The easy fix for my program: when doing this sort of bilocal analysis, ignore cells like R2C8 that have cyclic edges with more than two labels. By ignoring them, we don't make certain deductions that we might be able to, but it doesn't happen very frequently and when it does it will be caught by the later repetitive cycle rule anyway.