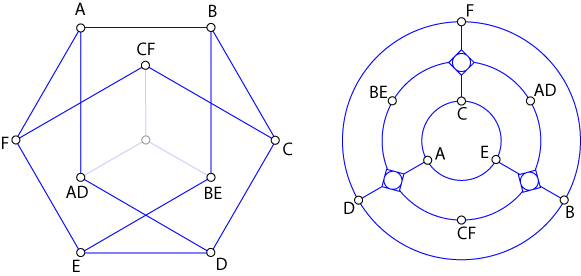
A confluent complement
Henk Meijer has described the confluent graph whose complement isn't confluent, and it's quite simple. In fact, the nonconfluent part was in our first paper on confluence: the Petersen graph, minus a vertex, is nonconfluent because it's nonplanar (a subdivision of \( K_{3,3} \)) and has no 4-cycles, so no way for confluence to gain traction. It turns out that its complement is confluent: