Two trees on integer partitions
From any partition of n, one can get a partition of n - 1, by subtracting one from the last value in the partition and removing it if it becomes zero. Connecting any two partitions related in this way forms an infinite tree, in which the nodes on level n represent the partitions of n:
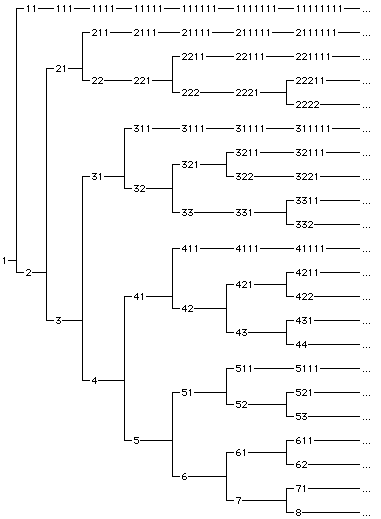
My recursive lexicographic and reverse-lexicographic-order partition generators work by traversing this tree (using a self-recursive BFS pattern, but a level-limited DFS would work just as well); they're efficient, even though they traverse a lot of lower-level nodes that aren't part of the output, because the number of nodes in the tree increases by a constant factor at each level.
On the other hand, there's another way to form a finite tree out of the partitions of n only: from any partition with two or more values in it, form a shorter partition in which the largest two values in the partition have been replaced by their sum, and connect the pairs of partitions so related.
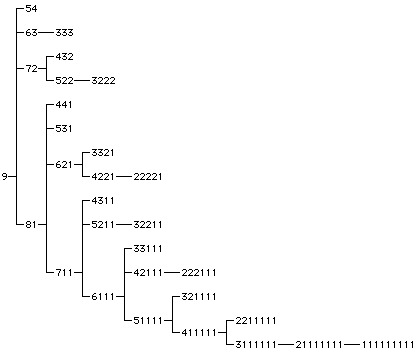
It looks like a depth first preorder traversal of this tree should provide an efficient generator for partitions in reverse colexicographic order, and a depth first post-order traversal of the reversed tree should generate partitions in colexicographic order. Terminating these traversals early would list the partitions using only values larger than some cutoff, or the partitions that use at least one value below the cutoff. The maximum value in a partition decreases as we progress down the tree, so we can list all partitions that have maximum larger than some cutoff by traversing the subtree they form. Breadth first traversal would list partitions in order by their length, but I don't know how to do this in a way that's efficient both in time and in space; iterative deepening (or the equivalent self-recursive BFS) doesn't work so well because the tree has too many of its nodes too close to the root. Instead, to list partitions in order by their length, efficiently, one can use Hindenburg's algorithm described by Knuth for listing partitions of each possible length, separately, but unfortunately I don't know of a nice way of relating this to tree traversals...