Bandwidth vs breadth-first search
Another new preprint of mine recently appeared: “Bandwidth vs BFS width in matrix reordering, graph reconstruction, and graph drawing”, arXiv:2505.10789, with Mike Goodrich and his student Alfred Liu. For me, it started with a mistake.
Mike had worked with several past students, including Pedro Matias, Marta Osegueda, and Ramtin Afshar, on reconstructing the connectivity of an unknown network by queries that find distances or shortest paths between vertices, such as you can get for internet nodes using the traceroute program. Any \(n\)-vertex bounded-degree connected graph can be reconstructed with \(\tilde O(n^{3/2})\) distance queries, but with unbounded degree the problem becomes evasive, unable to be solved with fewer than quadratic queries, because it is difficult to distinguish a star from a star plus one more edge: you cannot find the extra edge without querying its endpoints.
So Mike, Alfred, and I were holding a research discussion where we tried to push the subject even farther by looking for some combination of bounded degree and a bounded width parameter like treewidth that might allow fewer queries than the general bounded-degree method. A natural graph parameter to use here is bandwidth: a graph has bounded bandwidth if its vertices can be arranged into a sequence so that each edge connects vertices a bounded distance apart in the sequence. Unlike treewidth, this implies bounded degree. And it occurred to me that, at least for graphs of bounded bandwidth, we could get a linear number of queries: use queries between one vertex and all others to arrange the vertices in a breadth first layering, which obviously would have a bounded number of vertices per layer, and then use queries between all pairs of vertices in the same or consecutive layers to reconstruct the graph. But it is not obvious and it is not true: breadth first layering of bounded-bandwidth graphs does not always produce a bounded-bandwidth vertex sequence.
We later discovered that the same idea of using breadth first search to approximate bandwidth had already been tried long ago. It is the main idea of the Cuthill–McKee algorithm from sparse numerical linear algebra, which has the goal of permuting a symmetric matrix into a form where all the nonzeros are close to the main diagonal. Both this algorithm and the related “reverse Cuthill–McKee algorithm” start with a breadth-first layering of a graph describing the structure of nonzeros of a given matrix, and then apply more careful ordering heuristics within each layer. But it doesn’t approximate the bandwidth to within a bounded approximation ratio, and any such approximation would imply that \(\mathsf{NP}\) is contained in quasipolynomial time, a highly unlikely consequence.
We discovered the mistake in our graph reconstruction algorithm by finding a graph of bandwidth two for which the BFS layering could produce layers of logarithmic size:
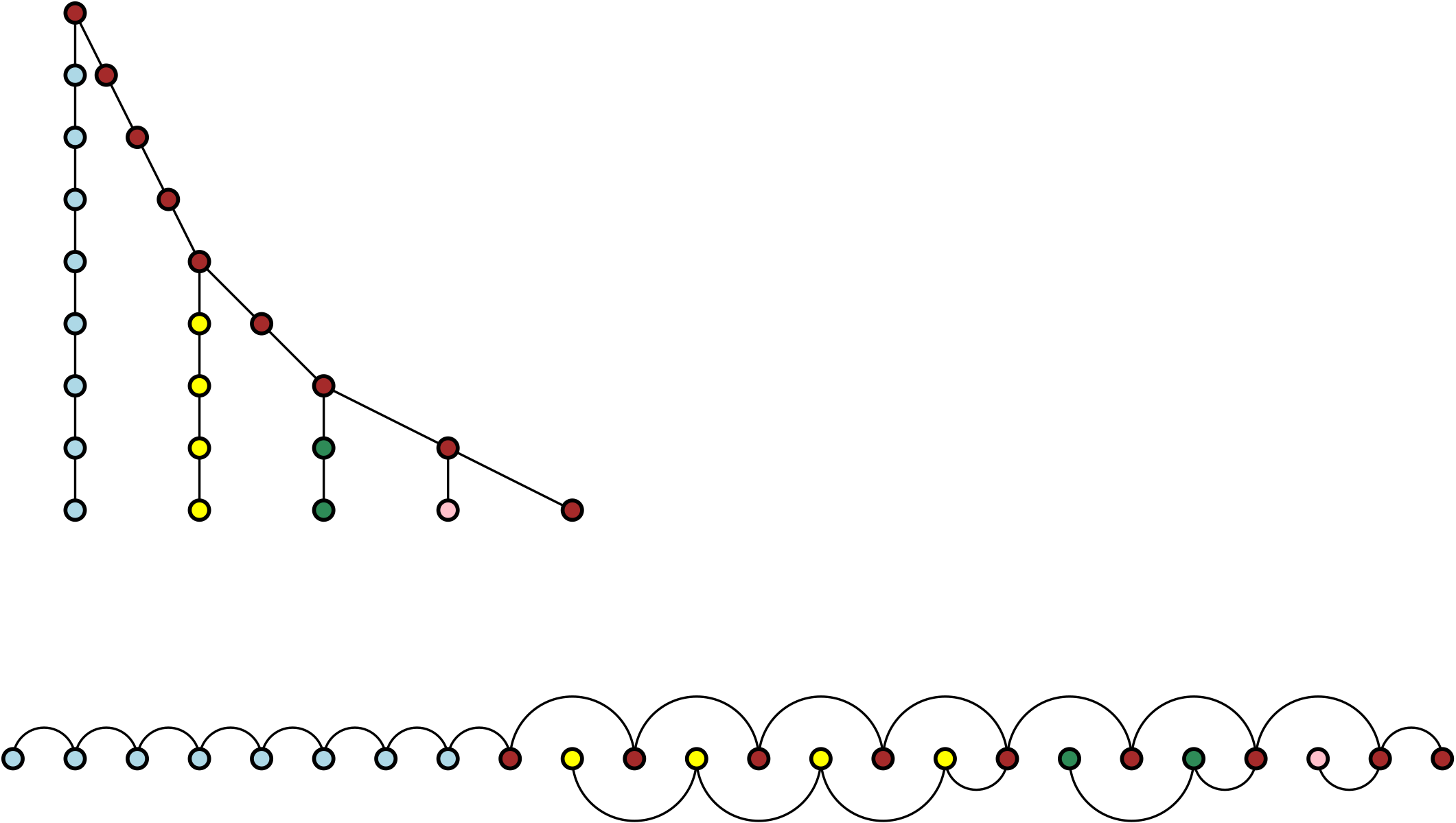
This example shows, among other things, that Cuthill–McKee algorithm gives at best a logarithmic approximation to the matrix bandwidth problem it aims to solve, but that logarithmic approximation gap also turns out to have been known long ago. Fortunately, we did not stop there. By applying the same hierarchical structure as this example recursively, we found that, for every integer \(k\), there exists a bound \(b_k\) on the bandwidth such that some graphs of bandwidth \(b_k\) have layerings with \(\Omega(\log^k n)\) vertices per layer. And then, by studying the recursive structure of these examples, we were able to show that all bad examples have basically the same structure, or can be massaged into this form without reducing their badness. This gave us a matching upper bound on this approximation method: for every integer \(b\), there exists a number \(k_b\) such that all BFS layerings of all graphs of bandwidth \(b\) have \(O(\log^{k_b}n)\) vertices per layer. To summarize: breadth first layering (and its more refined special cases, the Cuthill–McKee algorithm and reverse Cuthill–McKee algorithm) produces a polylogarithmic approximation for the bandwidth in graphs of bounded bandwidth, with an exponent that grows with the bandwidth. But our bounds are not tight enough to determine for each bandwidth the exponent of its polylogarithm.
I think the application to sparse numerical linear algebra is more important than the application to reconstructing graphs from probes, but the summary for the probing problem is not far from the mistaken linear bound that kicked this off. If we reconstruct a graph by using queries from a single vertex to construct a breadth-first layering, and then query all pairs in the same or consecutive layers, we can reconstruct any graph of bounded bandwidth in \(\tilde O(n)\) queries. The \(\tilde O\) hides a polylogarithmic factor coming from the connections we made between bandwidth and BFS, whose exponent depends on the assumed bandwidth bound.