End-of-year linkage

Harvard allegedly shut down a research project on disinformation in Facebook ($\mathbb{M}$) by noted social scientist Joan Donovan after getting a big donation from the Zuckerbergs (far outweighing the $12M Donovan had raised for the project) and planting a Facebook “fixer” on a dean’s advisory council. Donovan, a research scientist at Harvard since 2016, has since moved to a tenure-track faculty position at Boston University.
Academic publishers: please just let us download pdf files rather than making us use your advanced enhanced viewers.
A function that, when iterated twice, triples its argument. Working out its values makes a fun puzzle.
A new lower bound for sphere packing ($\mathbb{M}$). In a new preprint, Campos, Jenssen, Michelen, and Sahasrabudhe improve the asymptotic density of sphere packing by a $\log d$ factor, the first such improvement since 1947.
A Cairo pentagonal tiling, or an elaboration of one, in a 15th-century mosque in Cairo ($\mathbb{M}$). If the tiling itself has the same date, this is much earlier than both the 17th-century Mughal examples and the mid-20th-century Cairo street pavers listed in the Wikipedia Cairo tiling article.
The largest polyominoes with no $k$ equally-spaced cells on a straight line. New investigations by Alexandre Muñiz based on a 2020 preprint by Jan Kristian Haugland.
Real-life fractal tree zoom ($\mathbb{M}$), created using 3d printing by Henry Segerman. Part of the trick to getting it to work well involves finding a fractal with a small expansion factor.
One of my favorite pieces of public art in Palo Alto, “Body of Urban Myth” (Brian Goggin, 1997; $\mathbb{M}$) is now accessible only from the outdoor dining area of a Sicilian restaurant near the courthouse. Fortunately it’s not difficult to enter the area in the afternoons before they open:
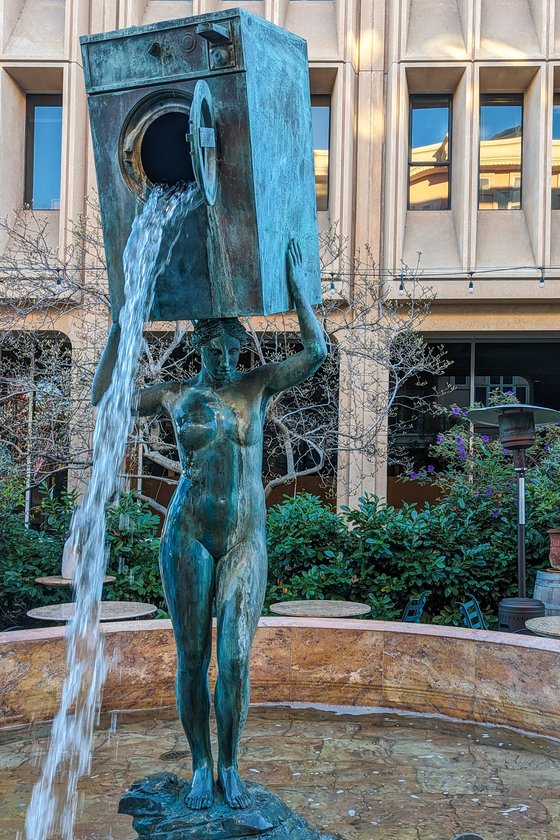
The well-covered graphs ($\mathbb{M}$) have the property that you can can find maximum independent sets in them by an easy greedy algorithm: just start with the empty set and keep adding vertices that are independent of the ones you’ve already added until you get stuck. A maybe familiar example: add rooks to a chessboard, none attacking each other, until no more rooks can be added. You will always fill all the rows and columns exactly once, placing exactly eight rooks. So the rook’s graph is a well-covered graph. Now a Good Article on Wikipedia.
Wikimedia Russia is shutting down ($\mathbb{M}$) after its executive director, Stas Kozlovsky, an associate professor at Moscow State University, was essentially fired from his professorship for being declared a foreign agent, and after its previous executive director was banned from Wikimedia projects for helping the Russian government make a fork of Wikipedia. Note that this is Wikimedia Russia (the official support organization for Wikipedia etc in Russia), not the Russian-language Wikipedia. I don’t see any possibility that the Russian-language Wikipedia will stop existing, but accessing it or contributing to it from within Russia may be difficult or dangerous.
Another new Wikipedia Good Article: Hyperbolic spiral ($\mathbb{M}$). These are less familiar mathematically than the famous self-similar logarithmic spirals, but you’ve seen them before: every time you look up a spiral staircase, the projected plane view that you see is a hyperbolic spiral. They’re also used for the starting positions of footraces, so that the runners take the same distance to reach the finish line.
Coq theorem prover moving ahead with rename to Rocq ($\mathbb{M}$) after a 2022 survey found it to be the most popular replacement name. See also a long discussion of alternatives and reasons for change, which explains that Rocq is short for Rocquencourt, where the prover was first developed, and that juvenile humor based around the old name (by some accounts an intentional aspect of its original choice) had been used to sexually harass female users causing them to leave the project.
Square roots on the Curta, from Chris Staecker’s 12 Days of Curtsmas video series ($\mathbb{M}$). Matt McIrvin explains more about the the square root algorithm.
Bringing eclipsed women of astronomy and physics into the light ($\mathbb{M}$). In Symmetry magazine, Madeleine O’Keefe reviews Shohini Ghose’s new book Her Space, Her Time.
Claude Bragdon: Drawings of the Fourth Dimension (1913-1915) ($\mathbb{M}$, via).
Numbers too big for our universe ($\mathbb{M}$). Dick Lipton and Ken Regan write in “Gödel’s Lost Letter” on vector addition systems, problems in which you start with a non-negative integer vector and repeatedly add vectors from a given set, staying non-negative and seeking to reach zero. In 1976, Lipton showed that this is EXPTIME-hard, but results of Czerwiński, Orlikowski, and Leroux in two FOCS 2021 papers, recently summarized in Quanta, show that it’s much worse, requiring Ackermann-function time and space.