Mid-November Linkage

We recently installed a wall-mounted scratching pole (\(\mathbb{M}\)) to give our kittens access to the space above the bathroom false ceiling (to the upper left of this photo) and the lintel between the bathroom and bedroom (upper right). It’s their new favorite place.

Suppose five points \(a\), \(b\), \(c\), \(d\), and \(e\) are chosen at random, independently and uniformly, on a unit sphere. What is the probability that the circle through \(a\), \(b\), and \(c\) separates \(d\) from \(e\) (\(\mathbb{M}\))? As I was walking to my computational geometry class one of the students caught up to me and described this problem. They said it was from an IMO but if so I think I must have misunderstood the problem, because it’s too easy. Spoilers in discussion thread.

Animated trajectory of the Lucy space probe and its complicated sequence of gravity boosts on its mission to visit eight asteroids.

Formalizing recent research in Ramsey theory (\(\mathbb{M}\)) using the Lean theorem prover, by Bhavik Mehta.

Medium appears to be paywalling basically everything. Dorothea Salo suggests that this prevents work there from being used as course readings, but the same goes for social media links. It is becoming a write-only medium. Put your work somewhere more open if you want people to link to it and read it.

USSR is in \(\mathsf{P/poly}\) (\(\mathbb{M}\)), by Nikhil Balaji and Samir Datta. No, this is not about Soviet politics. “USSR” is the problem of determining the sign of an expression formed by adding and subtracting integer square roots, when the numbers are specified in unary. Such expressions arise, for instance, when you want to compare the perimeters of two polygons with integer vertex coordinates. The complexity of the problem with binary inputs is a notorious open problem in computational geometry. This paper almost settles the problem for a restricted case with smaller coordinates (or with more time for larger coordinates). Almost because it’s \(\mathsf{P/poly}\) rather than \(\mathsf{P}\): this means that there is a program that solves the problem in polynomial time, given access to a polynomial-length “cheat sheet” for each input size. The cheat sheet length is not enough to precompute the answers to all possible problems; instead the paper converts the problem into one of evaluating a linear threshold function, and applies an old result of Saburo Muroga on the existence of small integer reweightings of threshold functions that produce the same result. The integer weights of Muroga’s reweighted threshold function are what go onto the cheat sheet.

Corollaria Gyroid (\(\mathbb{M}\)), behind the design and construction of an abstract mathematical sculpture in the Albany Airport in the form of an aluminum gyroid surface perforated by a centroidal Voronoi tessellation.

Greg Egan animates Dini’s surface, a helical trumpet-like surface with uniform negative curvature, and the patch of the hyperbolic plane that it is isometric to. This patch grows arbitrarily large as the helical boundary of Dini’s surface is wound more tightly. So although the entire hyperbolic plane has no smooth embedding in \(\mathbb{R}^3\), any bounded subset of it does. In practice, the limit on the size of a subset that can be embedded will be set by the thickness of your hyperbolic paper: the volume of paper needed to embed a patch of radius \(r\) grows exponentially with \(r\) while the volume of space that the same patch of paper can reach grows only cubically.

A short video on pasta extrusion (\(\mathbb{M}\)). As Dan Piker points out, different parts of the pasta may leave the die at different rates, causing the extruded surface to be non-developable.

What makes a constructive proof (\(\mathbb{M}\))? The issue arises in questions where one can provide an explicit construction of a solution, but the proof of correctness of the construction involves an excluded middle. Lance provides an example in complexity theory, a 2014 result constructing a language in the complexity class \(\Sigma_2^{\mathsf{P}}\) (the second level of the polynomial hierarchy) that does not have circuits of size \(n^2\), but with two different proofs of its correctness: one that works if SAT has small circuits, and another that works if no such circuit exists. Discussion on the linked thread centers on the difference between enumeration and effective enumeration in constructive versions of Cantor’s uncountability proof.

Coxeter’s embedding of the Pappus configuration on a torus with a few alternative views with varying torus proportions, Leah Berman. The same configuration also embeds nicely on the flat square torus (with crossings, so not Coxeter’s embedding) and on the flat hexagonal torus (Coxeter’s embedding):

37 is the median second prime factor (\(\mathbb{M}\)) of uniform random integers in the range \([1,N]\), in the limit as \(N\to\infty\).

Notable enough? The questioning of women’s biographies on Wikipedia (\(\mathbb{M}\), via), a study by Franziska Martini of deletion discussions on the German-language Wikipedia. She concludes that women’s biographies are more often called into question than men’s, and “discussed more controversially”, but not deleted more often. She attributes these gender differences to collective bias rather than individual misogynistic editors. The German Wikipedia has different standards for who to write articles about, but I think at similar levels of fame/accomplishment to the English Wikipedia, with similar processes, and many of her conclusions probably carry over.

The ridiculous path my university thinks pedestrians should follow to avoid walking in the road (\(\mathbb{M}\)) after one of its construction sites (covering most of the right side of the image) closed the only sidewalk connecting one side of the faculty housing complex (bottom of image) to the main campus (top of image):

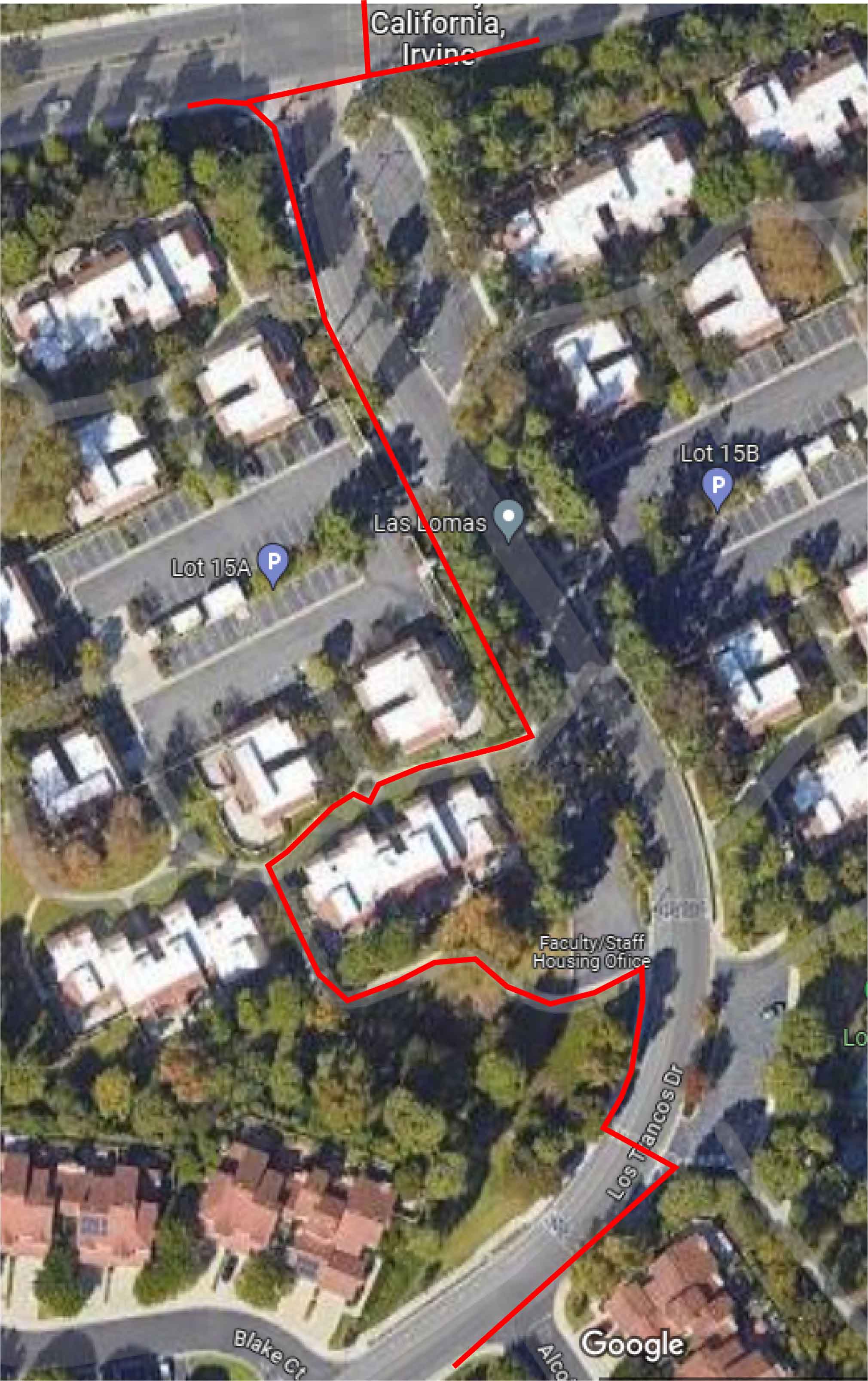
The Knotology of Heinz Strobl (\(\mathbb{M}\)), Paula Versnick, Orihouse. Knotology is like 3d geometric origami but made from paper strips instead of paper squares.