Soddy's quadlet
Soddy’s hexlet is a famous system of nine spheres in three-dimensional Euclidean space, consisting of a ring of six spheres, tangent in consecutive pairs, and a ring of three spheres, tangent in pairs, with every sphere in one ring tangent to every sphere of the other ring. The easy way to construct it is to observe that its properties are invariant under Möbius transformations, as long as you count planes as spheres, and parallel planes as tangent spheres. If you take two of the three spheres in the three-sphere ring to be parallel planes, the rest have to form seven congruent spheres, six of them in a ring around the seventh. Any other form of the hexlet can be obtained by a Möbius transformation from this one.
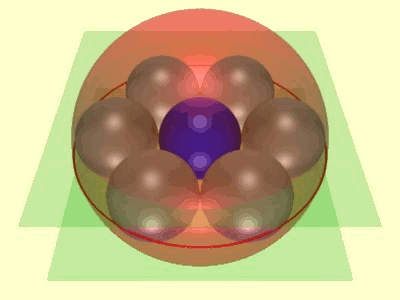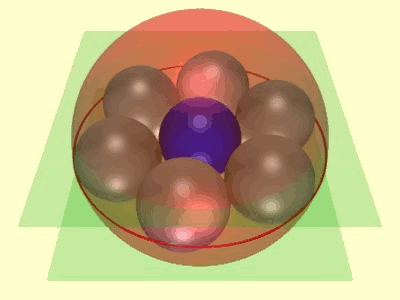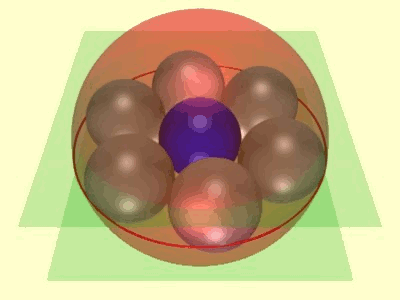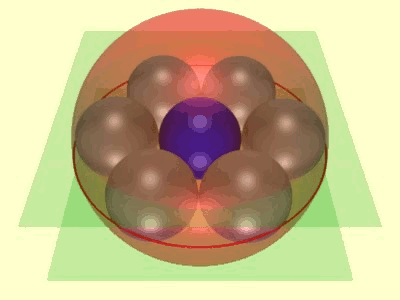
But there’s another way of constructing the same shape, coming from four-dimensional polyhedral geometry, which can also be used to construct another related pair of interlocking rings of spheres.
By analogy, consider a cube in 3d, and start growing a sphere with its center at the center of the cube. As you grow the sphere, it will start to bulge out through the faces of the cube, which cut it in six circles. Initially, those circles will be small and disjoint from each other, but as they grow larger they will eventually touch at the midpoint of a cube edge, and then cross each other. At the time when any two of the growing circles touch each other, all six will touch four others, by the symmetries of the cube. In this way, we have generated a configuration of six circles, on the surface of a sphere, each touching four others with the same touching pattern as the square faces of a cube.

Now do the same thing in 4d with the (3,6)-duoprism, the Cartesian product of an equilateral triangle and a regular hexagon. The resulting 4-dimensional polytope has facets of two type: six triangular prisms (attached to each other on their triangle faces) and three hexagonal prisms (attached to each other on their hexagon faces). Rectangular faces connect triangular prisms to a hexagonal prism. There is a choice for how big to make the triangle edges relative to the hexagon edges. You want them to be in the proportion \(\sqrt3:1\), so that both kinds of prism have an inscribed sphere touching all their faces. Instead, the only figures I could find of the duoprism show it with edges in the wrong proportion \(1:1\), generating square faces. But I want the rectangular one.
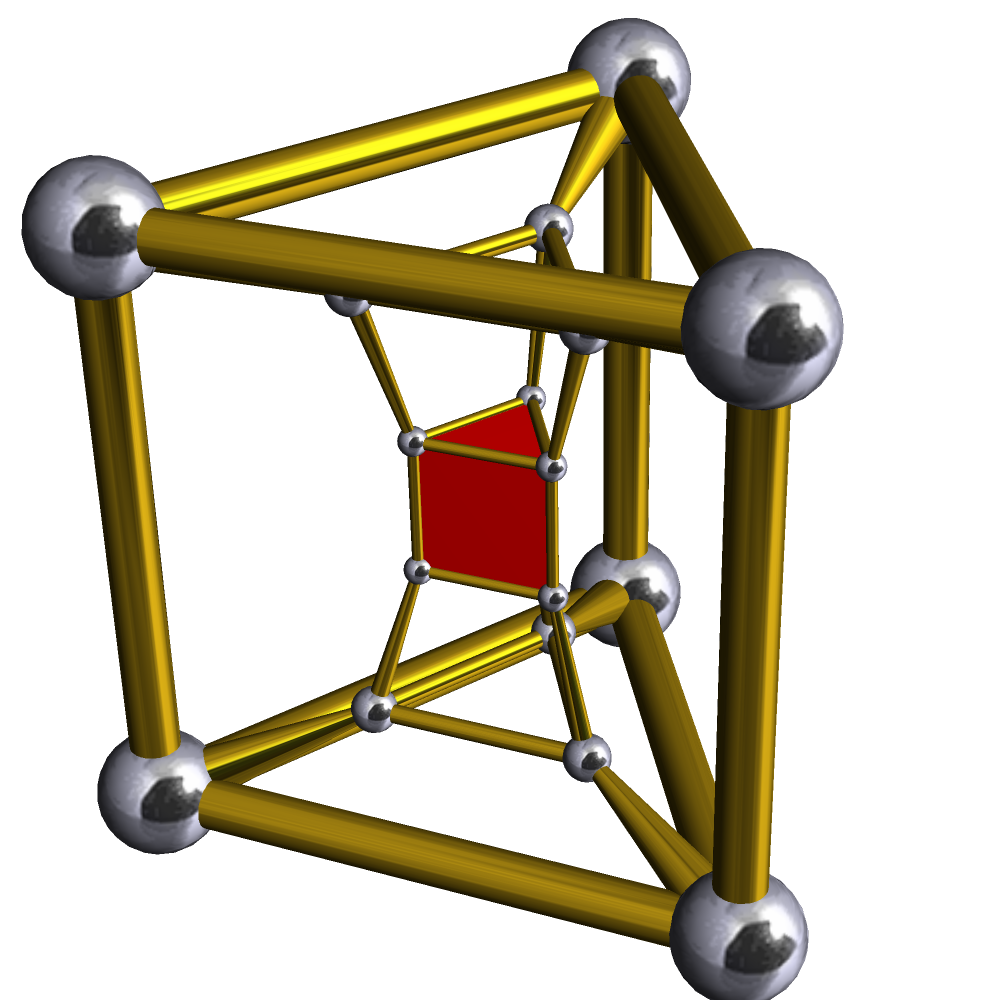
Grow a hypersphere from the center of the duoprism. As it grows, it will intersect the prism facets of the duosphere in spheres, centered at the centers of the prisms. Initially small and disjoint, these spheres will grow until they become the inscribed spheres of the prisms, touching each other at the center of each triangle, hexagon, or rectangle of the duoprism. You have created a hexlet, simultaneously drawn on a sphere and inscribed in the faces of a duoprism! You can map it into the usual hexlet of three-dimensional Euclidean geometry (instead of three-dimensional spherical geometry) by a stereographic projection from the hypersphere to a flat three-dimensional space.
Almost all the other duoprisms do not have this coincidence, that when you adjust the proportions to make one kind of prism have inscribed spheres, the other one does the same thing with the same proportions. There’s only one other duoprism for which this works: the (4,4)-duoprism, better known as the 4-hypercube or tesseract. In this case, all the facets are the same, and all the 2-faces are the same. If we grow a hypersphere, centered at the center of the hypercube, it will cross the hypercube facets (which are cubes) in spheres. When these spheres grow to the size where they are inscribed in each cube facet, they will be tangent to each other at the centers of the square two-dimensional faces of the hypercube. At this point, you will have formed two rings of four tangent spheres, tangent in consecutive pairs, with every sphere in one ring tangent to every sphere of the other ring. We could call it the “quadlet”.
Now that you’ve constructed a quadlet on a hypersphere in 4d, you can apply a stereographic projection to get the same quadlet as a collection of ordinary spheres in 3-dimensional Euclidean space. One of the more symmetric ways of doing this projection takes one of the two 4-sphere rings to two unit spheres sandwiched between two parallel planes at distance 4 from each other. The four spheres of the other ring all have radius 2, and wrap around the central two unit spheres. It’s not obvious to me that these two parallel planes, two unit spheres, and four radius-2 spheres can all be tangent in this pattern, unless we calculate the coordinates of their tangencies or use reasoning based on the spheres inscribed on the facets of a hypercube, for which the same pattern of tangencies is obvious.
You can rotate the four radius-2 spheres around the axis formed by the central unit spheres arbitrarily without changing the pattern of tangencies. This is more or less analogous to the fact that with the hexlet, you can start the ring of six tangent spheres at any sphere tangent to all three spheres of the other ring, and then add spheres to the ring one by one, keeping each sphere tangent to its predecessor in the same ring and to all the spheres of the other ring. It will always close up after six spheres to form a hexlet. You can also fix in place the six-sphere ring, choose any sphere tangent to all of them to start the three-sphere ring, and it will always close up after three spheres to form a hexlet. And once you have one of the four-sphere rings of a quadlet, you can choose any sphere tangent to all four to start the other ring, and it will always close up after four spheres to form a quadlet. For the hexlet, this becomes obvious after we do a Möbius transformation to take it into the form with two parallel planes and seven congruent spheres. For the quadlet, it is similarly obvious by doing a Möbius transformation to take it into a form with two parallel planes in one ring and four congruent spheres in the other. The only way for the remaining two spheres to complete the first ring is for them to fill the hole between the four congruent spheres, one directly on top of each other. They might not be the same size as each other but one more Möbius transformation makes them so. So just like the hexlet, all quadlets are Möbius-equivalent.
Incidentally, the fact that you can get systems of three-dimensional tangent spheres from four-dimensional polytopes is not particularly new. I used it long ago in my paper with Kuperberg and Ziegler, “Fat 4-polytopes and fatter 3-spheres”, to get a finite set of spheres with high kissing number from the 120-cell and its relatives. For more on the connection between sphere packings and 4-polytopes, including the construction of the hexlet from the duoprism, see Hao Chen’s papers and especially “Apollonian ball packings and stacked polytopes”.