Linkage

The early history of continued fractions (\(\mathbb{M}\)). Includes the equivalences of infinitude with irrationality and periodicity with quadraticness, and the work of Euler and Gauss on continued fractions for values with nice series expansions.

According to EHESS, Pierre Rosenstiehl has died (\(\mathbb{M}\)). I don’t think I met or interacted with Rosenstiehl, but I definitely interacted with his works: he was one of the founders of the International Symposium on Graph Drawing and co-editor in chief of the European Journal of Combinatorics, with important publications in topological and algorithmic graph theory on bipolar orientations and the left-right planarity test.

Aerial photos of the year, 2020 (\(\mathbb{M}\), via). The link shows only the “man-made” category; be sure to click on all the others as well.

Simulation and visualization of the large-scale structure of the universe (\(\mathbb{M}\), via), including webs of dark matter and the transition from an opaque early universe to its present mostly-transparent state.

The cocked hat (\(\mathbb{M}\)). This interestingly-titled recent preprint by Bárány, Steiger, and Toledo concerns locating yourself by measuring angles to three landmarks. Usually, random error causes rays from the landmarks to form a triangle rather than meeting at a point. Supposedly this triangle contains your position with probability 1/4, but the preprint shows that this can be proven only for distributions that force the rays to form a triangle. See also Toledo’s new book, Location Estimation from the Ground Up.

MDPI is asking its authors to spam Wikipedia with their work (\(\mathbb{M}\)), and so is Elsevier. I’m not surprised by MDPI doing this but, despite my low opinion of them, I thought Elsevier were better than that.

Drawing machines (\(\mathbb{M}\), via). An archive of optical/mechanical/automated drawing machines/devices/aids.

Origami Fibonacci torus and knotted torus (\(\mathbb{M}\)). I have the impression that the Fibonacci part just gives it a nice organic look, visible in much of Akio Hizume’s other architecture, but what interests me is the way it rotates smoothly. That’s not something unfolded paper can do, because the inner parts of a torus have negative curvature, the outer parts are positive, and unfolded paper can’t change curvature.

The floorplan below is of the KölnTriangle, a building in Cologne which has been claimed to be a Reuleaux triangle in cross-section (\(\mathbb{M}\)). Obviously it’s not. The Torre de Collserola in Barcelona looks much more promising but a published description of its specific architecture would help make that more clear.

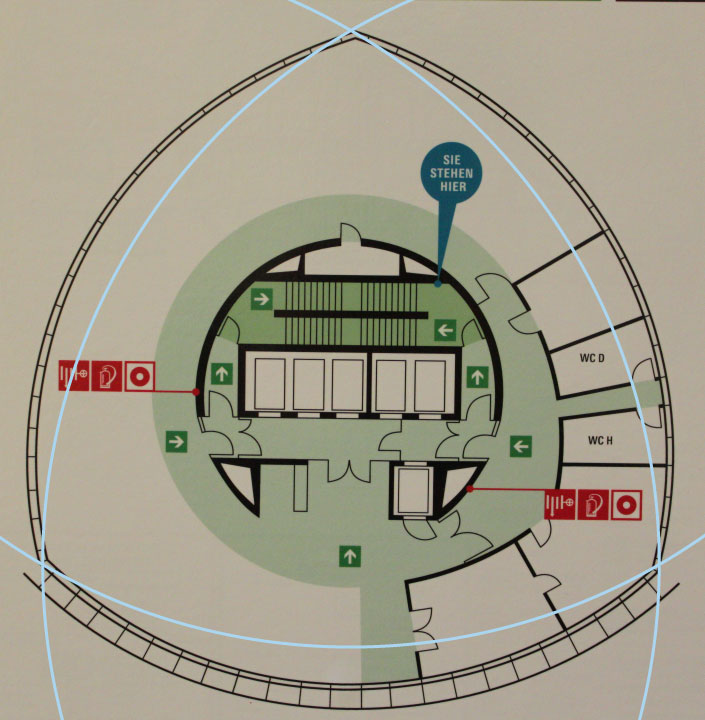
The Complexity Zoo needs a new home (\(\mathbb{M}\)). Scott Aaronson’s collection of complexity classes and their relations had been at the U. Waterloo Institute for Quantum Computing, but their bureaucrats have decided that they cannot accept the liability of it possibly being out of compliance with accessibility rules, without allowing him to fix any issues or even tell him what issues it might have. As Scott writes, “Do you find it ironic that a central effect of these accessibility policies seems to be to make free academic content less accessible than before?”

Two more recent deaths in discrete mathematics and theoretical computer science (\(\mathbb{M}\)): Robin J. Chapman, problem-solver extraordinaire (and scarily almost exactly the same age as me), and Dave (C. L.) Liu, early researcher in scheduling algorithms and VLSI layout and later president of National Tsing Hua University (Chinese-language obituary).

Contortion engineering (\(\mathbb{M}\)). Engineering-style drawings of Escher-like impossible objects. An old link from my old Geometry Junkyard site — its old earthlink url went dead some time after 2016, when archive.org last captured it, but now it has a new home.