Linkage

Should graduate students be expected to bring refreshments to their doctoral defenses? (\(\mathbb{M}\)). It can be an imposition, it distracts from preparing from the defense, students on graduate fellowships may not easily afford it, and to some extent it looks like bribery of the examining committee. On the other hand, it’s traditional and it’s hard to break traditions, and a non-hungry committee is a non-hangry committee.

Some places have resorted to banning student-provided refreshments, and/or providing refreshments through other means. For our most recent defense, what we ended up doing was less extreme: we made sure the candidate understood that we were not expecting treats and that he should only bring them if he wanted to (which it turns out he did) and we reimbursed the expenses.

Stop using Zip Codes for geospatial analysis (\(\mathbb{M}\), via). The problem is that they are designed to be convenient for the post office (geographically compact) rather than convenient for demographers (they sometimes combine areas that have quite different groups of people in them). The linked article is by a group selling software for one alternative subdivision that works better, but recommends several others as well.

Minimal representations of order types by geometric graphs (\(\mathbb{M}\)). How should one visualize the order-type of a set of points (which triples are clockwise, which counterclockwise, and which collinear)? Aichholzer et al consider points without collinear triples, and draw a graph over the points so that as points move the order-type changes only as points cross edges. Their graph’s embedding determines the order type and has at most a third as many edges as the complete graph.

Properties of the affine curve-shortening flow (\(\mathbb{M}\)). Gabriel Nivasch asks MathOverflow for references on the behavior of this process for self-intersecting curves.

Mow your lawn using the power of math (\(\mathbb{M}\)). This piece on optimal lawn-mowing seems to be unaware of prior work on the same subject (Fekete et al, “The Lawnmower Problem”, CCCG 1993). But it has some interesting suggestions about the possibility of an art installation with grass covering a Möbius strip.

Trump administration threatens to shut down scholarships, societies, and even summer camps that promote women in STEM, claiming that they discriminate against men (\(\mathbb{M}\)). Note: Not The Onion.

To make two black holes collide, try three (\(\mathbb{M}\)). The recent discovery of gravity waves from black hole collisions has led to the realization that these collisions are surprisingly frequent: two-body problems are sufficiently stable, even under general relativity, that pairs of black holes should continue orbiting around each other for eons rather than crashing. As Quanta describes, one possible resolution is to add a third black hole to the mix, and get a (significantly less stable) three-body problem.

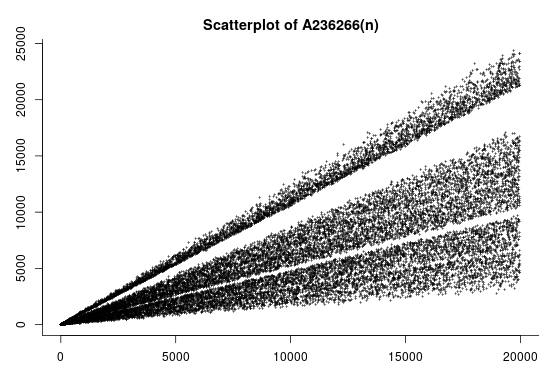
The greedy no-3-in-line sequence (\(\mathbb{M}\), via). This is what you get when you try to solve the no-3-in-line problem by choosing, for each non-negative integer \(x\), the smallest non-negative \(y\) avoiding lines through previous points. Its scatterplot suggests that this greedy algorithm finds subsets of \([n]^2\) of size \(\Omega(n)\), even though this method is very different from the constructions for which this density has been proven.

Dutch academics fear language rule would hinder foreign recruitment (\(\mathbb{M}\), see also, see also, see also). Many Dutch universities have been teaching entire programs of study in English, and the Eindhoven University of Technology is English-only. A proposed law would outlaw that; not unreasonably, the Dutch universities are worried that this change would make it harder to recruit students from other countries.

New database of self-citation (\(\mathbb{M}\), via). There are legitimate reasons to self-cite (as the article makes clear) but when senior researchers have a majority of citations from their own papers, and then get government awards for being highly cited, there’s likely a problem. Or more than one problem, both in the researcher’s citation habits and in the criteria for the awards.

Why do academic talk slides conventionally cite the speaker using only an initial? And how would one go about achieving that effect in BibTeX?

Pandrosion (\(\mathbb{M}\)), a woman in ancient Greek mathematics prior to Hypatia. New article on Wikipedia.