Big convex polyhedra in grids

I recently wrote here about big convex polygons in grids, a problem for which we know very precise answers. This naturally raises the question: what about higher dimensions? How many vertices can be part of a convex polyhedron in an \(n\times n\times n\) grid, or more generally a convex polytope in a \(d\)-dimensional grid of side length \(n\)? Here we do still know some pretty good answers, at least up to constant factors in spaces of constant dimension.

The problem is included in a 2008 survey by Imre Bárány,¹ according to whom the maximum number of vertices is

\[\Theta\left(n^{d-2+\frac{2}{d+1}}\right).\]

For instance, in three dimensional \(n\times n\times n\) grids the maximum number of vertices is \(\Theta(n^{3/2})\).

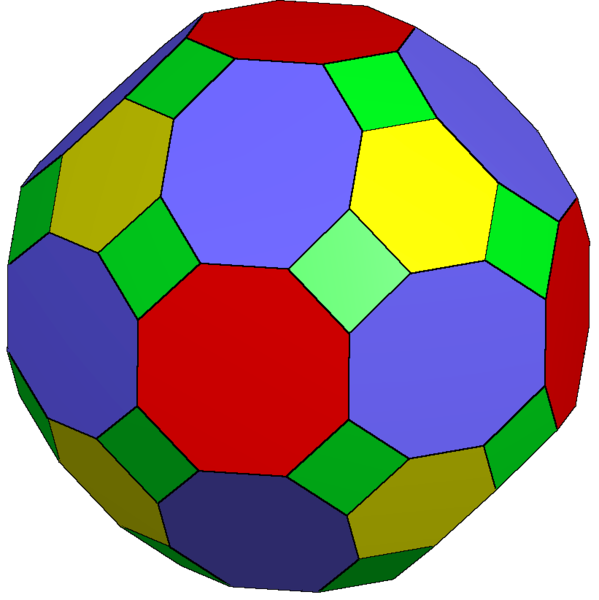
One way to find polyhedra with this many vertices is to take the convex hull of the points in a ball,^{2 3} or in scaled copies of any fixed smooth convex body. Another way, which should generate polyhedra with a somewhat less irregular appearance and (up to constant factors) the same number of vertices, is to take the Minkowski sum of all line segments (up to scaling and translation) that will fit into a smaller grid, of side length \(O(n^{1/(d+1)})\). For instance, the truncated rhombicuboctahedron below⁴ is the Minkowski sum of all the line segments that fit into a unit cube. Its 96 vertices lie in a \(10\times 10\times 10\) grid. In general, this method produces a zonohedron whose complexity can be analyzed in terms of a \((d-1)\)-dimensional arrangement of \(O(n^{d/(d+1)})\) hyperplanes. As long as this arrangement is not too degenerate (which it appears not to be, but I haven’t worked out the details carefully) this should give a number of vertices within a constant factor of the number coming from the convex hull construction.

A matching upper bound comes from a 1963 paper by G. K. Andrews,⁵ and Bárány writes that although several more proofs have been published none of them is easy. I’m not sure whether the difficulty is in getting the exact bound or in the fact that Andrews and the later proofs allow more general shapes with volume \(n^d\) that don’t fit into a grid, but it’s not hard to get close to the right bound simply by counting the number of possible facets of a given volume \(v\). By using lattice basis reduction the integer vectors in the hyperplane through any facet have a nearly-orthogonal basis whose product of lengths is proportional to \(v\). By considering how this product of lengths can be broken down into factors of different scales, and counting how many integer vectors of those lengths exist, it follows that the number of possible facets of volume \(v\) is \(O(v^d\log^{d-1} v)\). Combining this with the \(O(n^{d-1})\) surface area of a grid polytope gives the correct upper bound on the number of vertices up to a polylog factor.

What about when the dimension is not constant? An easy construction for high dimensions is to take all points with a fixed distance \(r\) from the grid center. There are \(O(dr^2)\) possible values for the distance, so this construction produces a convex polytope with \(\Omega(n^{d-2}/d)\) vertices. It comes from a 1946 paper by Behrend, who uses this idea to find dense sets of integers with no arithmetic progressions.⁶ It is never worse to use the convex hull of the ball than the points on a sphere, and a celebrated paper by Elkin from 2011 (in the appendix of the published version) gives another proof of the \(\Omega(n^{d-2+2/(d+1)})\) bound for convex hulls of balls (for \(d\ge 5\)) in which the constant factor of the \(\Omega\) is universal, not depending on \(d\). So when \(n\) is singly exponential in \(d\), \(n^{2/(d+1)}\) becomes constant and the convex hull technique produces \(\Omega(n^{d-2})\) vertices, improving Behrend’s construction for progression-free sets by the same \(d\) factor.⁷

(Discuss on Mastodon)