Peeling vs shortening
My latest preprint is about two processes, one continuous and one discrete, that appear to do the same thing as each other. We don’t really understand why. The preprint is “Grid peeling and the affine curve-shortening flow”, with Sariel Har-Peled and Gabriel Nivasch (arXiv:1710.03960) and will appear at ALENEX.
The discrete process is the one where you find the convex layers of a grid, or a subset of a grid. That is, you find the convex hull, remove its vertices, find the convex hull of the rest of the points, remove its vertices, etc. I wrote about it briefly a month ago, in a G+ post on a related integer sequence. When you do this to a square grid, the layers appear to get more circular as you go inwards (until they become so small that being on a grid forces them to get more polygonal again). When you do it to a rectangular grid, they appear to get elliptical. And when you do it to a quarter-infinite grid…
…you appear to get a hyperbola. What’s going on?
The continuous process is a variant of the curve-shortening flow called the affine curve-shortening flow. It operates on smooth curves in the plane, by moving all the points of the curve simultaneously. Each point moves towards its local center of curvature, at a speed proportional to the cube root of the curvature (the inverse of the cube root of the radius of curvature). If you take the “cube root” part out, you get the curve-shortening flow, under which every simple closed curve instantaneously smooths itself, then more slowly becomes convex (while avoiding self-intersections), then slowly becomes more circular (while shrinking to a point). The affine curve-shortening flow does much the same thing, more slowly, but it becomes elliptical instead of circular.
What we noticed was that if \(C\) is a convex curve, then affine curve-shortening on \(C\) and the convex layers of the points of a fine grid inside \(C\) appear to be much the same. Here’s an example where the initial curve is less symmetric than a square or rectangle. The left side is affine curve-shortening, the right side is grid peeling, and the middle is a much coarser grid peeling (with every fifth layer shown) to demonstrate what we’re doing. Can you tell the difference between left and right?
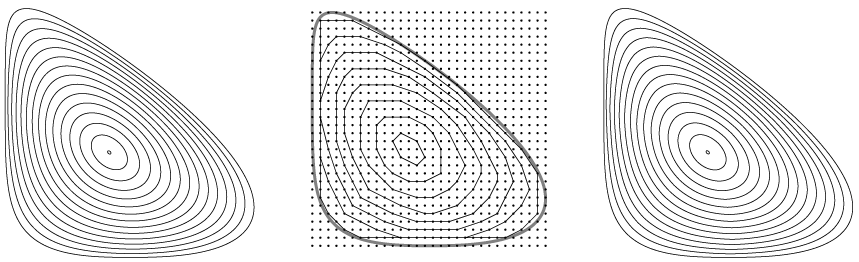
Of course proof by picture is not very convincing. We have some theory to support this observation (we can prove that grid peeling moves within a constant factor of the speed of affine curve shortening) and some vague heuristic arguments for why they might be the same (grid peeling is invariant under a big subset of affine transformations, so if it’s going to act like a flow it should be a flow that’s also affine invariant, and the simplest choice is affine curve-shortening). But we did send this to a conference about experiments, so we also did some experiments to see how similar the two processes are.
The answer: pretty similar, similar enough to convince us that (in the limit as the grid becomes finer) grid peeling converges pointwise to affine curve-shortening. See the preprint for the details, but the basic story from the experiments is that for fine grids the Hausdorff distance between the peeled grid curves and the affinely shortened curves is small, and grows smaller with finer grids. Decreasing the grid spacing by a factor of 10 decreased the Hausdorff distance by a factor of about 2.65, so that suggests that the distance is a sublinear power of the grid spacing, but that’s a wild extrapolation from two data points so it would probably be a mistake to guess the exponent with more than one digit of precision.
Anyway, maybe this is easy to prove, to someone who has the right theoretical tools in hand (which is not us).
(G+)