Stable redistricting in road networks
I have another arXiv preprint, “Defining Equitable Geographic Districts in Road Networks via Stable Matching” (arXiv:1706.09593, with Mike Goodrich, Doruk Korkmaz, and Nil Mamano). It’s a follow-up to our previous work on stable matching in grids, but this time in road networks.
The idea is to partition a geographic region (such as a US state) into smaller districts from a given set of centers, so that each center has an equal (or designated) proportion of the population, and everyone is near their center. We formulate it as a stable matching problem where each center should be matched to its quota of population points, represented as vertices in a road network. Each center prefers to be matched to people near it and vice versa. Here’s an example of the kind of partition you get out of this:
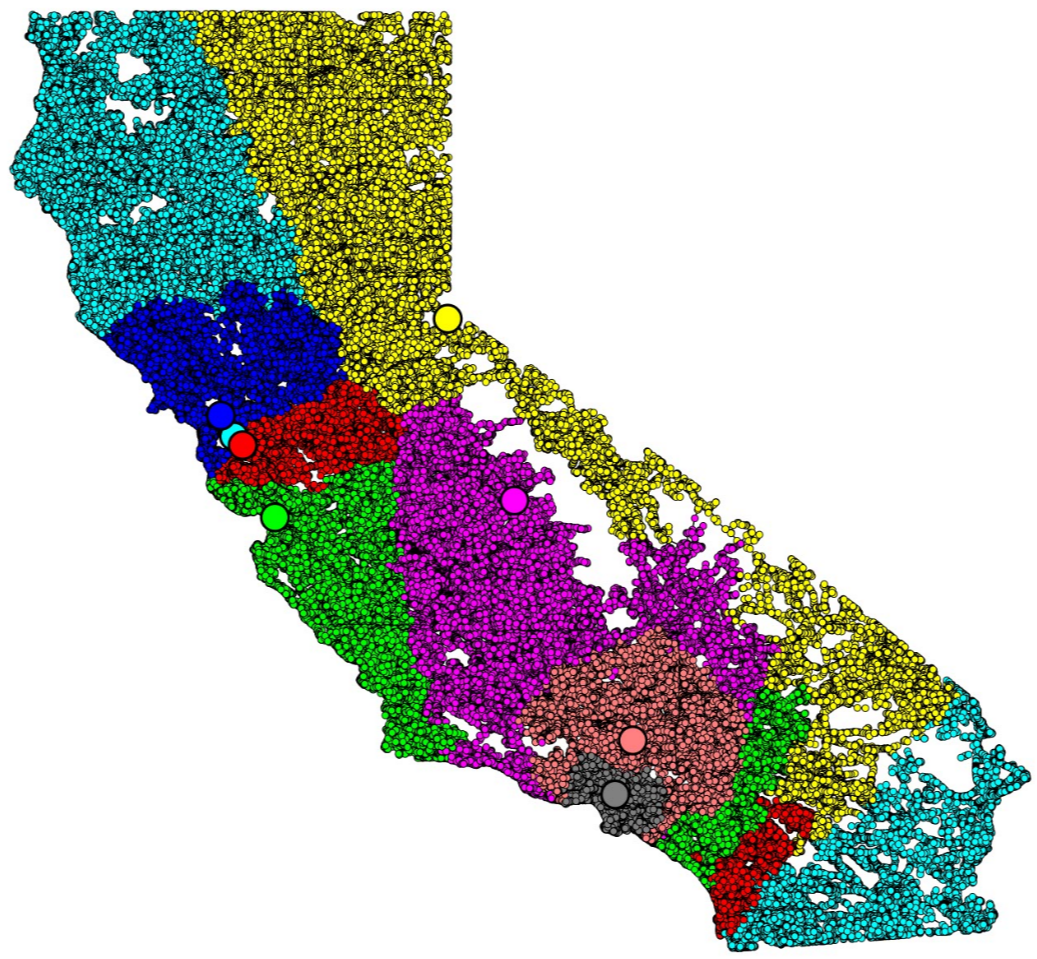
This shows a partition of California into eight districts with random centers. The blank spots on the map are places roads don’t go (mostly mountains and desert). You can see that there are some problems with the partition, such as the light blue center somewhere in the San Francisco Bay Area getting most of its area in the far north and far south of the state. That sort of disconnection wouldn’t be allowed in the applications we have in mind, such as congressional redistricting. We hope to fix those sorts of issues by a more careful choice of centers, or possibly also by relaxing the requirement that each center have exactly the same quota, but for now we’re just investigating how to compute this partition.
It turns out that stable matching problems such as this one, where symmetric distance functions are used to determine the preferences on both sides of the matching, have unique solutions that can be constructed by a variant of the nearest-neighbor chain algorithm from hierarchical clustering. We already used this idea in our grid matching paper, but it was easier there because of the existence of efficient dynamic post office data structures for points in a grid. To generalize this algorithm to road networks, we need a dynamic graph algorithm that can maintain a changing subset of network vertices and find the nearest neighbor in the subset to any query point, efficiently. This turns out to be possible using a separator hierarchy, giving us an algorithm to find the matching in time \(O(n^{3/2}\log n)\) for \(n\)-vertex networks.
This is better than the classical Gale–Shapley algorithm when the number of centers is large, especially because running Gale–Shapley requires computing and storing distances from all vertices to all centers, a slow and memory-consuming task. Using the nearest-neighbor chain method we were able to solve some partitioning problems on which other algorithms ran out of memory. However, our computational experiments showed that for most inputs a better and simpler algorithm than either Gale–Shapley or the nearest neighbor chain algorithm is possible. The idea is to interleave multiple instances of Dijkstra’s algorithm, one for each center, matching each point of the graph to the first instance of Dijkstra that reaches it, and stopping each instance when it reaches its quota. One can find inputs that cause most of the instances of Dijkstra’s algorithm to search most of the graph, so the worst-case runtime of this interleaved Dijkstra method matches the distance computation phase of Gale–Shapley. But in our experiments with random centers most of the instances of Dijkstra’s algorithm stopped early, giving us fast running times in practice.
It seems reasonable to hope that, under some assumptions about what the input looks like and with randomly chosen centers, the interleaved Dijkstra method can achieve near-linear runtime. But we were not able to prove this; it’s one of the problems we list as open at the end of the preprint.