What I mean by “cage” is that the edges and vertices of one polyhedron form a “cage” that encloses a solid polyhedron and prevents it from escaping to infinity by a continuous rigid motion.

The problem came up in a visit with some old friends, Michael and Jeanette Lee, over the Memorial Day holiday. The Lees have a third-grade son, Ian, who is fascinated by Menger sponges, and has a set of snap-together squares with which he can make small ones. He asked: how big a cube can be enclosed by the edges of another cube?

On the face of it this seems similar to a question I asked years ago, on how small one could make a cube that fits inside a unit cube and touches all its faces. Maybe taking the solution to that problem and scaling it up works?

Box in a box

But no, that’s no good. If you try this you will get stuck with a caged cube that’s exactly the same size as its cage, forming the compound of two cubes:

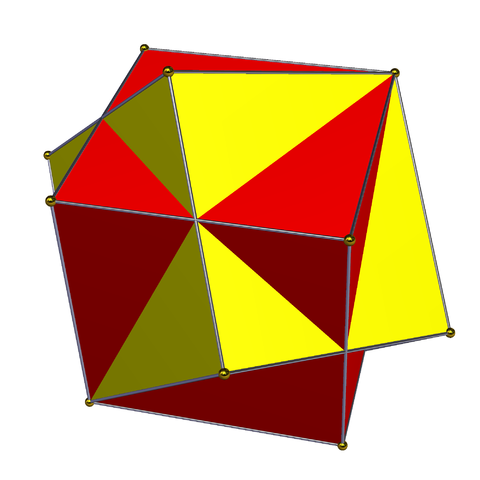
Compound of two cubes, from File:Compound two cubes.png on Wikimedia commons

And in fact this compound does not even form a cage! The solid cube can rotate around the shared axis of the cubes until it is aligned with the hollow cube that is supposed to be caging it, and then slither out through one of the square sides of the hollow cube. It doesn’t seem possible for a cube to cage a larger cube, despite examples like Prince Rupert’s cube by which a cube can have a hole large enough for a larger cube to pass through. It also doesn’t seem possible for a regular tetrahedron to cage another regular tetrahedron. But I have no proof of these claims.

I was able to find cuboids that can cage larger copies of themselves. For instance, when \(x\approx 1.1,\) a \(1\times x\times x^2\) cuboid can cage a cuboid that is bigger by a factor of \(x^2\approx 1.2,\) by lining up the two cuboids so that their length-\(x^2\) edges are parallel but with one cube rotated around an axis parallel to those edges so that, in cross-section, the corners of the smaller one protrude just beyond the sides of the larger one.

Caged cuboid

The fact that two of the corners protrude noticably more than just beyond the sides makes me think that this construction is not very tight. Are significantly larger scale factors possible for self-caged polyhedra? And can we prove that a cube can’t cage a larger cube?

(Google+)