Face incidence polytopes

In my previous post here I remarked that the hypercubes are the face lattices of simplexes. I also drew the face lattice of a square, which you might have noticed forms a planar graph, the graph of another polyhedron (the tetragonal trapezohedron, an octahedron with eight kite-shaped faces). This turns out not to be a coincidence. For every many (see comments) \( d \)-dimensional convex polytopes \( P \), the covering graph of its face lattice is the graph of a \( (d+1) \)-dimensional convex polytope, which for lack of a better name I'll call the face incidence polytope, or incidence polytope for short (although that shorter phrase does already have a different meaning).

This polytope shares more structure with \( P \) than just its vertex and edge set. If \( P \) has an \( i \)-dimensional face that forms a subset of a \( j \)-dimensional face, then this incidence between the two faces of \( P \) corresponds to a \( (j-i) \)-dimensional face of the incidence polytope, and every face of the incidence polytope comes from an incidence of two faces of \( P \) in this way. In particular, the vertices of the incidence polytope correspond to the incidences between faces of \( P \) and themselves, and the edges of the incidence polytope correspond to incidences between faces that are one dimension apart, which form the edges of the covering graph of the face lattice.

Construction

The construction of the incidence polytope is very simple. Given a polytope \( P \), place \( P \) so that the origin of its space is interior to it, and let \( Q \) be its polar polytope. Place \( P \) and \( Q \) on two parallel \( d \)-dimensional hyperplanes in \( (d+1) \)-dimensional space. Translation or scaling of these two planes doesn't affect the combinatorial structure of the result, but it is convenient to choose how to place these two hyperplanes so that they are perpendicular to the line connecting their origins; neither polytope should be rotated. Next, construct the convex hull of the union of \( P \) and its parallel polar. Then, the incidence polytope is the polar polytope to this convex hull.

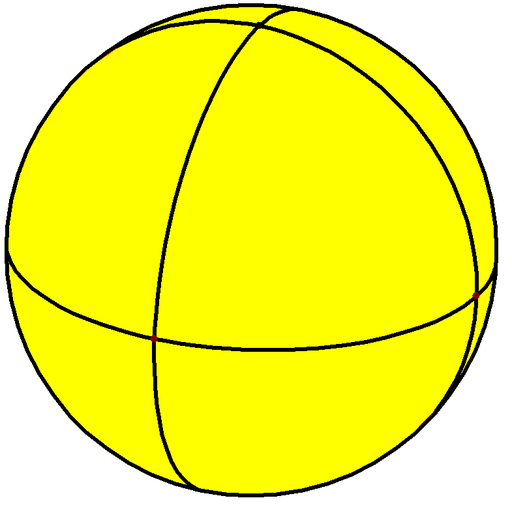
For instance, if you start with a regular polygon with \( n \) sides, then its polar polygon is also regular with \( n \) sides, but rotated by an angle of \( \pi/n \) with respect to the original polygon, so that the vertices of the two polygons interleave each other. Placing these two polygons on two parallel planes and constructing their hull gives an antiprism, and then forming the polar polytope of this antiprism gives us a trapezohedron, like the one I drew last time.

Correctness

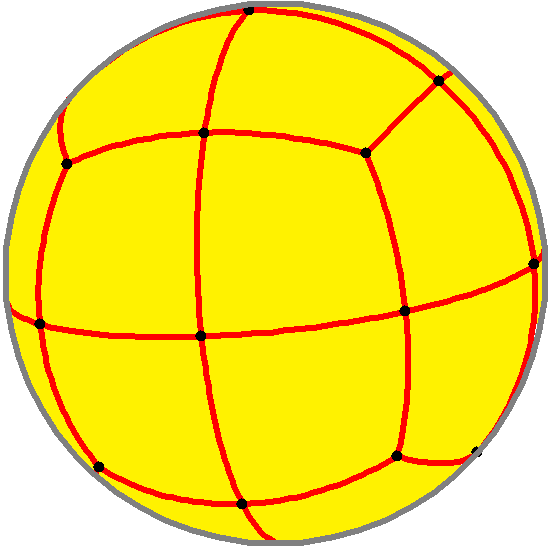
Why does this work? (When it works at all; see comments.) I think the simplest explanation involves dropping a dimension, to a \( (d-1) \)-dimensional (hyper)surface in \( d \)-dimensional space, the image of the Gauss map. This map transforms points on the surface of \( P \) to their (set of) unit normal vectors. The set of all unit vectors is a sphere, and the image of the Gauss map is a subdivision of the sphere according to which point or points of \( P \) are most extreme in a given direction. For instance, the Gauss map for a cube subdivides the sphere into eight spherical triangles. Each triangle corresponds to one of the eight vertices of the cube. The unit vectors in this triangle represent directions in which that cube vertex is the most extreme: its dot product with the vector is bigger than the dot products involving the other seven vertices.

The edges of this subdivision represent directions in which there are two equally extreme points (the endpoints of an edge of the cube) and the vertices of the subdivision represent directions in which there are four equally extreme points (the vertices of one of the cube's faces). In this way, the features of the Gauss map correspond to the features of the cube, but with the dimensions reversed. If instead we take the Gauss map of the polar of a cube (an octahedron), both the polar and Gauss map operations reverse dimensions and we get the cube itself back, but a spherical cube rather than a polyhedral one. And if we overlay the Gauss maps for the cube and its polar, we get something like this:

If we have a unit vector \( \mathbf{v} \) in \( (d+1) \)-dimensional space, then we can use this overlay diagram to determine the extreme points for the hull of the union of \( P \) and its offset polar. First, as a special case, if \( \mathbf{v} \) is parallel to the line between the origins of the two \( d \)-dimensional subspaces, we know the extreme points: they are either all of \( P \) or all of its polar, depending on the sign of \( \mathbf{v} \). Otherwise, we can project \( \mathbf{v} \) to a nonzero vector in the two subspaces, and look it up which cell of the overlay diagram contains it; this will tell us the extreme points for \( P \) and its polar in the direction of \( \mathbf{v} \). The extreme points for the hull of \( P \) and its polar can only be the same as the extreme points for \( P \), for its polar, or both, because a hyperplane perpendicular to \( \mathbf{v} \) that touched any other points of \( P \) or its polar would cut through the hull and separate some extreme points from the rest of the polytope. So this means that the only faces (sets of extreme points) that we can obtain are the ones coming from features of the overlay diagram, which are exactly the ones we want.

Applications

In my previous post we saw that the faces of the hypercube are in one-to-one correspondence with the sets of binary strings that can be described by placing wildcards in some positions of the string, and fixing other positions to 0 and 1. In order to make this correspondence work, we needed to include one more set of binary strings (the empty set) that could not be described by wildcards in this way, to correspond to the empty \( (-1) \)-dimensional face of the hypercube. The incidence polytope construction shows that these wildcard strings (together with \( \emptyset \)) are also in one-to-one correspondence with the vertices of a polytope, the incidence polytope of a hypercube. The edges of the incidence polytope represent the ways in which you could turn a 0 or 1 into a wildcard character or vice versa.

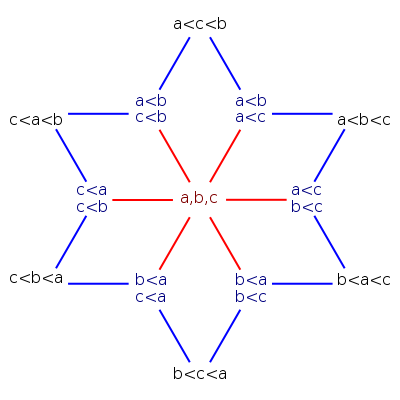
Another polytope whose faces are meaningful is the permutohedron, the convex hull of the permutations of the vector \( (1, 2, 3, \dots, d) \). It's a \( (d-1) \)-dimensional polytope, because these points all lie in a hyperplane (their sum of coordinates is a triangular number). Its nonempty faces correspond to weak orderings, orderings that like the outcome of a horse race are transitive (if \( x \) beats \( y \) and \( y \) beats \( z \) then \( x \) beats \( z \)) but may have equivalence classes of tied elements: the vertices of a face are the permutations that can be formed from the ordering by breaking all ties in a consistent way. Here for instance are the 13 weak orderings of a three-element set:

The 3-element permutohedron is a regular hexagon. The outer six vertices of the diagram above correspond to the hexagon's vertices, the middle six vertices correspond to the hexagon's edges, and the central vertex corresponds to the whole hexagon. So we have here almost the entire face lattice of the hexagon, but we're missing one vertex, corresponding to the empty set. If we add back this one vertex (adjacent to the six outer vertices of the diagram) we get the graph of a polyhedron, the hexagonal trapezohedron, the incidence polyhedron of the hexagon. In the same way, if we take the incidence polytope of a permutohedron, we get a \( d \)-dimensional polytope whose vertices represent all the weak orderings of a \( d \)-element set (with one extra vertex representing the empty set of permutations, or an inconsistent weak ordering). The edges of the incidence polytope represent ways of breaking a tie by splitting one equivalence class into two smaller equivalence classes.

In the same way, the nonempty faces of an associahedron represent partial parenthesizations of a sequence, or partitions of a regular polygon by sets of diagonals into smaller convex polygons; its vertices represent complete parenthesizations or triangulations of a convex polygon. The vertices of the incidence polytope of the associahedron also represent partial parenthesizations, or partitions into convex polygons, except for one extra vertex representing the empty face of the associahedron. The edges of the incidence polytope represent ways of inserting one more pair of parentheses or one more diagonal.

Comments: