Typically, computational problems that are straightforward for computers are also straightforward (but possibly tedious) for people, and vice versa. For this reason, the puzzles that people find intellectually challenging tend to be NP-hard or worse. But this is not always the case: some computational problems have algorithmic solutions that are simple when measured by computational complexity, but difficult when measured by the ability of people to actually perform (or implement) them. A case in point is the problem of finding planar embeddings of graphs, which forms the basis of the Planarity puzzle. In this puzzle, you are given a tangled drawing of a planar graph, and must untangle it by moving the vertices. This is easy for computers — linear time algorithms have long been known — but still a bit of a challenge for people.

In solving Planarity puzzles by hand, I've found that a simple strategy works pretty well: find a short cycle such as a triangle or quadrilateral, assume that it's a face, and then build adjacent faces one at a time by finding short paths that connect pairs of vertices on the boundary of the already-found faces. It's easy to come up with examples of planar graphs where this strategy leads you into mistaken choices very quickly, but it doesn't happen when I play it. I've also found that the partial embeddings of this strategy can be kept neat by placing the vertices within a tightly packed grid, with irregular boundaries but no empty space inside the packing, and that by making small changes to the grid placement most or all puzzles can be embedded in such a way that each vertex is adjacent only to vertices among the eight grid neighbors reachable by a single move of a chess king, as shown in the example below. Again, this is very far from true for all planar graphs — the nested triangles graph is a counterexample — but it seems to be true for the graphs the Planarity puzzle uses. At first I thought this meant that Planarity generated its graphs from grids, with some random choice about which diagonals to use, but that turns out not to be true.

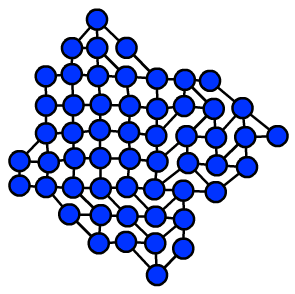
Planarity puzzle, Level 8, solved with each two vertices a chess king's move apart

My new preprint, "Drawing Arrangement Graphs In Small Grids, Or How To Play Planarity" (to appear at Graph Drawing 2013, arXiv:1308.0066) is my attempt to explain these observations mathematically. It turns out that the graphs used by Planarity are formed from randomized line arrangements. Based on their construction, I can show that the simple greedy algorithm outlined above, of adding short cycles one at a time as faces to a partial embedding, always works for these graphs. Additionally, although I can't show that they can be packed into grids without any wasted space or long edges, I can show that they can have grid packings with significantly less wasted space than arbitrary planar graphs would need.

Of course, this only works for arrangement graphs. There are some other clones of the original Planarity puzzle out there, that use other graphs, and the strategies from my preprint wouldn't work for them. It might be interesting to try to characterize types of graphs that are particularly hard to solve: for instance, my greedy algorithm would fail on graphs that have many short non-facial cycles, as the nested triangles graph does. Another interesting direction to go from this would be to find other random processes than line arrangements that lead to interesting subclasses of the planar graphs to use for these puzzles.