A median graph of 213-avoiding permutations
If you make a graph with a vertex for each permutation of length \( n, \) and an edge for two permutations related by a swap of adjacent values, it looks like this:
It has some nice properties: it's a Hamiltonian partial cube with isometric dimension \( n(n-1)/2, \) and the graph of an \( (n-1) \)-dimensional polytope (the permutohedron) There's an easy way to compute distances in this graph (count the inversions). But what if we consider a subset of the permutations, the ones avoiding the permutation pattern \( 213 \)?
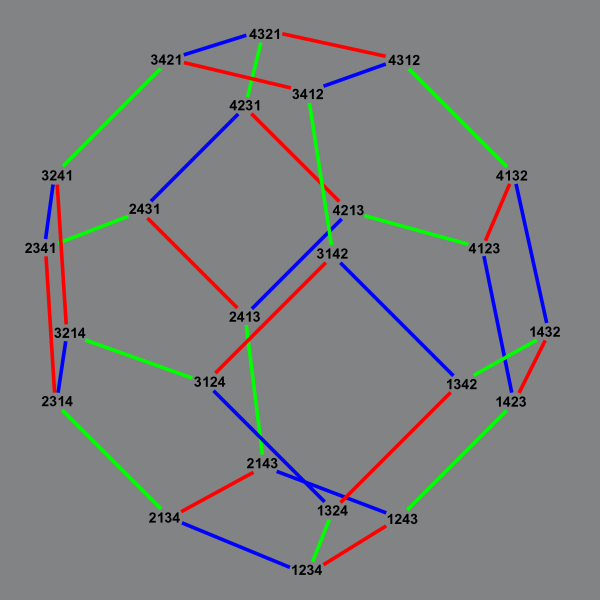
We get an induced subgraph of the permutohedron, but not an isometric subgraph: its distances may be very different. Here's what it looks like for \( n=5: \)
(The colors come from a recursive construction in which the graph is decomposed into Cartesian products of smaller graphs of the same type, one for each possible position of the \( 1 \).)
This turns out to also have nice properties, but different ones. It has a Catalan number of vertices, and a Fibonacci number of degree-one vertices. (The degree-one vertices all either start with \( 1 \) or start with \( 2 \) and end with \( 1, \) and are degree-one vertices in the smaller graph of swaps on the remaining subsequence after removing these boundary values, from which we get the Fibonacci recurrence.) And it's again a partial cube, but more strongly a median graph. That is, every three \( 213 \)-avoiding permutations \( x, \) \( y, \) and \( z \) of the same length have a unique median \( m(x,y,z) \) that lies on a shortest path between each pair.
I think the easiest way to show that this is a median graph is to express it as the system of solutions to a 2SAT problem. Given a \( 213 \)-avoiding permutation \( p \), define an upward set of \( p \) to be a set \( S \) of two or more elements of the permutation that occur in ascending sorted order in \( p, \) with the additional property that, if the second-largest element of \( S \) is \( x, \) no element smaller than \( x \) can be added to \( S \) while preserving this sorted property. For instance, the permutation \( 654321 \) has no upward sets, but the permutation \( 651243 \) has five: \( \{1,4\}, \) \( \{1,3\}, \) \( \{1,2\}, \) \( \{1,2,4\}, \) and \( \{1,2,3\}. \) The set \( \{2,3\} \) is in ascending order in this permutation, but is not an upward set, because it is part of a larger set \( \{1,2,3\}. \) If you know the upward sets of a permutation, you can identify the permutation itself, as the largest and second largest element of each of these sets tell you which pairs of elements you need to swap relative to the downward-sorted permutation. Again, in the same example, to get the permutation \( 651243 \) from the downward permutation \( 654321, \) we should swap pairs \( 14, \) \( 13, \) \( 12, \) \( 24, \) and \( 23 \) (but only those pairs).
In a \( 213 \)-avoiding permutation, if \( x \) is any element, then the elements that are smaller than and left of \( x \) must be in ascending order and the upward sets with \( x \) as largest element must be formed by adding \( x \) to prefixes of this order. Therefore, if \( S \) and \( T \) are upward sets with the same largest element \( x, \) then either the remaining elements of \( S \) must form a prefix of the remaining elements of \( T \) or vice versa; any other pair of sets \( S \) and \( T \) are incompatible. If \( S \) is an upward set with three or more elements, then the set \( U \) formed by removing the second largest element is also an upward set (formed by the prefix with one fewer element). And if \( S \) is an upward set in which the largest two elements differ by more than one, then the set \( V \) formed from \( S \) by decrementing its largest element must also be upward, for the \( 213 \)-avoiding property implies that the decremented value can only be to the right of the second-largest value.
If a family of upward sets obeys these constraints and describes a permutation \( p, \) then \( p \) must be \( 213 \)-avoiding. For, if not, and elements \( x\lt y\lt z \) appear in \( x \) in order \( yxz, \) forming a 213 pattern, it would have an upward set whose largest two elements are \( xz, \) and repeated application of the decrement-max operation would lead to an upward set whose largest two elements are \( xy, \) which do not appear in that order in \( p. \)
Any family of upward sets that does obey these constraints does describe a \( 213 \)-avoiding permutation. By induction on the number of elements, the subfamily of upward sets that do not involve the largest element of the permutation describes a permutation on one fewer element. The position of the largest element can then be determined by the longest upward set \( S \) containing it. The remove-second-largest and decrement-max operations can be used to show that the set formed by removing the largest element from \( S \) must appear in sorted order at the start of the smaller permutation, from which it follows that adding the largest element to the permutation in the appropriate place gives the correct family of upward sets.
Therefore, if we make a 2SAT instance whose variables are the sets of two or more elements, with implications from \( S \) to \( U, \) to \( V, \) and to the negation of \( T, \) for each of the sets \( U, \) \( V, \) and each incompatible set \( T \) described above, then the satisfying truth assignments of this instance are exactly the families of upward sets of \( 213 \)-avoiding permutations, and the swap graph of these permutations is exactly the graph of single-variable changes to satisfying truth assignments. Since the graph of every 2SAT instance is a median graph, the swap graph of \( 213 \)-avoiding permutations is also a median graph.
The distance between any two permutations in this graph is the number of upward sets that belong to one but not both of them. The median of any three permutations can be found by choosing the family of upward sets that belong to at least two of them. And this method also allows us to immediately read off the isometric dimension of the graph of \( 213 \)-avoiding permutations on n elements: it is an Eulerian number, \( 2^n-n-1. \)