Moser spindle

The Moser spindle:

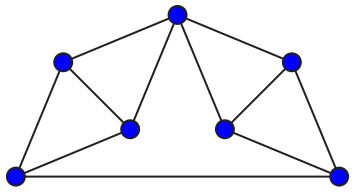
Despite being a named graph, it was previously only given a paragraph in the bigger Wikipedia article on the Hadwiger–Nelson problem, its main application, where it is used to show that one needs at least four colors to color the plane in such a way that no two points with the same color are a unit distance apart. But after seeing Peter Winkler's problem column in last month and this month's CACM I realized that it had enough other uses to warrant a separate article of its own.

The layout above shows that, as well as its usual embedding in the plane as a unit distance graph, it can also be embedded to form a pointed pseudotriangulation and therefore that it is a minimally rigid graph.