Compound of three octahedra

The compound of three octahedra, a shape formed by three regular octahedra rotated relative to each other, having symmetries taking any face to any other face. It was rediscovered independently by M. C. Escher, who used it as the central chameleon cage in his woodcut Stars.

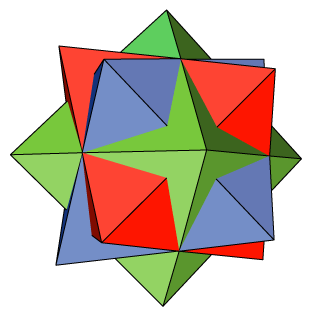
There's a hint of an Escherian illusion in Stars at the points where three octahedron edges cross each other, looking almost as if they cross each other at right angles. In the actual compound, the crossing angles are not perpendicular, but I wonder whether there's some hyperbolic form of the same compound in which they are.