Keller's cube-tiling conjecture and Keller graphs

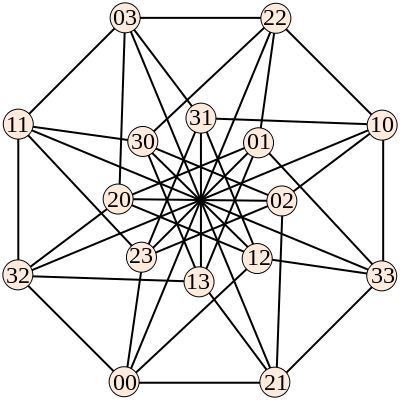
Keller's conjecture, a problem about the geometry of tilings of space by cubes, was resolved negatively by Lagarias and Shor in 1992. Along the way, it led to the discovery of the Keller graphs, a family of graphs that have made interesting and difficult test cases for clique finding algorithms. The calculation of the clique number of the 7th graph in this family (which turns out to have 2¹⁶ vertices and maximum clique size 124) was the subject of a SODA 2011 paper by Debroni et al.

Below is one of the graphs in this sequence, which turns out to be a relabeled version of the Clebsch graph.