Report from Graph Drawing
I just returned from Eindhoven, The Netherlands, where I participated in the 19th International Symposium on Graph Drawing. Some highlights:
There were two invited talks. The one by noted visualization researcher Jack van Wijk (who works in Eindhoven himself) featured many beautiful examples of graph-related visualizations, including regular maps embedded on 3d surfaces and a zoom into an adjacency matrix of a hierarchically clustered graph. One lesson I learned (from a user study by Holten et al in 2009) is that, when drawing directed graphs, edges that taper from the start to the end make for clearer drawings than the more traditional arrowheads, because you can see the directionality at any point along an edge. Günter Rote (who also had a contributed talk in the Lombardi drawing session) spoke about quantified versions of Steinitz's theorem according to which the graphs of convex polyhedra are exactly the 3-connected planar graphs. It's always possible to realize a graph of this type as a polyhedron with integer coordinates, and an interesting line of research has studied how big these integers need to be; the best known bounds are singly exponential, but stacked polyhedra can be realized with coordinates that are only polynomially large, and Rote seemed hopeful that this polynomial bound can be extended to the general case.
Kozo Sugiyama, an early graph drawing researcher who invented the Sugiyama-style layered drawing method, died recently. One of the sessions was dedicated in his honor, and Peter Eades delivered a moving eulogy for him at the start of the session.
In the technical session, I think the result most likely to interest people beyond the graph drawing circle was from a paper by Cornelsen and Karrenbauer, who used a separator-based divide and conquer to speed up minimum cost flows on planar graphs (with some technical restrictions involving bounded costs and bounded face degrees). They used their new flow algorithm to speed up the time for minimizing bends in planar orthogonal graph drawings to \( O(n^{3/2}) \).
Other contributed talks that I found particularly interesting included a user study by Greffard, Picarougne and Kuntz showing that when 3d drawings are combined with stereoscopic displays they can be more effective than 2d drawings; a proof by Mukkamala and Pálvölgyi that 3-regular graphs can always be drawn with all edges axis-parallel or diagonal; a bound by Suk on the number of edges in drawings with no k mutually crossing edges, using Davenport–Schinzel sequences; and two implementations of Lombardi-style drawings by Chernobelskiy, Cunningham, Goodrich, Kobourov and Trott showing that this style can be effective for arbitrary graphs, not just graphs with a high degree of symmetry. (Also noteworthy: Chernobelskiy and Cunningham are undergraduates.)
As usual, this year there was a graph drawing contest, with several components: graphs to be drawn ahead of the conference, graphs to be drawn by hand (using provided software) at a special session during the conference, and graphs to be drawn by automated software. Maarten Löffler and I entered one section of the pre-conference competition, involving a graph that was to be drawn with curves combining features of Lombardi drawing (optimal angular resolution at the vertices) and RAC drawing (right angled crossings). The graph was described as a circulant, with 15 vertices in a cyclic order, each connected to the vertices 1, 4, and 6 steps around the cycle. Our first drawing follows directly from this description. To make it, we used my LombardiSpirograph program on a planarization of the graph (with all crossings replaced by vertices) and then removed the extra vertices. My experience with this type of drawing is that it tends to work better to place the longer edges inside and the shorter edges outside, because it lets the vertices be spaced farther apart, so that's what we did.

Although this drawing is very symmetric, the graph itself turns out to be even more symmetric: it can be formed from five three-vertex independent sets, each of which is connected to two others by a \( K_{3,3} \) subgraph. So, while the drawing above has a symmetry group of order 30, the graph itself has a symmetry group of order 77760: the cycle of five triples can be rotated or reversed, and each triple can be permuted independently from the others. Because of this structure, the graph has only five maximal independent sets, each of size six, formed from two nonadjacent triples. We tried to show this structure in a planar drawing meeting the contest rules, but were unsuccessful. Instead, we submitted a second drawing showing this pentuple-\( K_{3,3} \) structure on a torus, with each triple of vertices forming one of the columns in a \( 3 \times 5 \) grid layout:
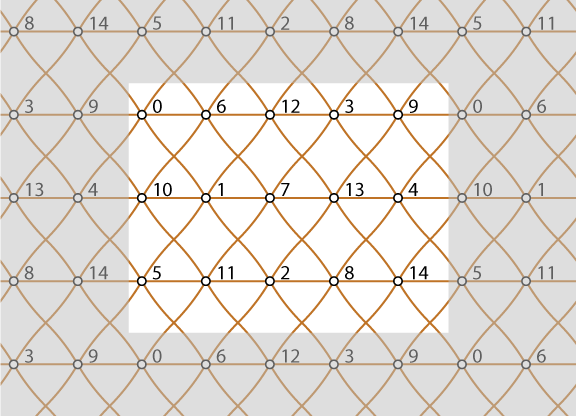
Another team entered a drawing very similar to our first one, but the second one tipped the contest in our favor, and we won. Maarten and Martin Nöllenburg also defended their honor in the hand-drawing competition, winning there for the second year in a row.
Unusually for Graph Drawing, there was a public business meeting. The main news items were that next year's symposium will be in Washington State, arranged by Lev Nachmanson, and that for next year's 20th anniversary celebration the contest will include a prize for the best computer game based on graph drawing. The schedule didn't allow much time for open discussion, probably just as well as this year also featured some political fireworks: an attempt to change how the steering committee is composed from its current old-boys-club dominated by permanent members to something more open and transparent. As with a similar attempt ten years ago, it seems to have failed, as the steering committee voted to maintain its own permanence. We also had a timidly-worded straw poll on whether someone should investigate open-access options for the conference proceedings; the results were overwhelmingly in favor of doing so.
The local arrangements featured a welcoming reception with plenty of food and good beer at a nearby pub, an Indonesian buffet dinner following the business meeting, a nicely raked auditorium with great acoustics and lines of visibility, a short walk to the conference site from the downtown hotels, and (as with the most recent WADS in New York) quite low registration fees. It makes me wonder what we're paying for in other conferences that have professionally-organized conferences with registration fees at least twice as high with worse facilities and less interesting banquets.