It's Graph Drawing proceedings deadline time, and not coincidentally my own papers from GD have all recently been uploaded to the arXiv.

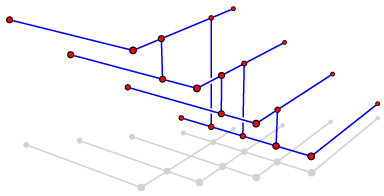
Hardness of Approximate Compaction for Nonplanar Orthogonal Graph Drawings (arXiv:1108.4705, with Michael Bannister) is on the problem of reducing the area requirements of grid drawings. The input is a drawing of a graph on an integer grid (with the edges running along paths through the grid edges) and the output is another grid drawing with a smaller bounding box, formed by moving the vertices either row-by-row or individually. It's not actually clear that this is a useful thing to do — it tends to make the drawings more cluttered looking — but it is at least a standard thing to do. Anyway this paper shows that it's also a hard thing to do: one can't get within even a \( \sqrt{n} \) factor of the optimal compaction in polynomial time, unless P=NP. The proof is a straightforward reduction from approximate graph coloring, but it turns out to be tight: there's a matching upper bound based on a greedy coloring algorithm. Here's a figure Michael had some fun drawing, of a 3d variant of the reduction:

Hardness reduction for 3d grid drawing compaction

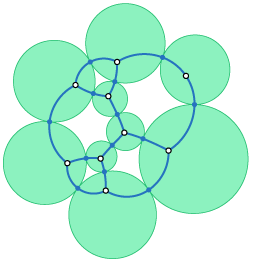
Planar and Poly-Arc Lombardi Drawings (arXiv:1109.0345, with Duncan, Goodrich, Kobourov, and Löffler) is a followup to our two papers from the previous year on Lombardi drawing, graph drawings with circular-arc edges and equally spaced angles at the vertices. Not every graph has a drawing of this type, so in this paper we relax the requirement that the edges be circular arcs, instead letting them be curves formed by joining two or more arcs. This turns out to make it much easier to construct the drawings and doesn't seem to hurt their aesthetics too much. The figure below illustrates one of our techniques, of constructing drawings with two smoothly-connected non-crossing arcs per edge for cubic planar graphs based on tangent circle representations of the input graph.

2-Lombardi drawing of a planar graph from its circle packing

Confluent Hasse diagrams (arXiv:1108.5361, with Joe Simons) combines the ideas of upward drawing (drawing a directed acyclic graph in such a way that all edges go upwards) and confluent drawing (eliminating crossings by routing edges together on train tracks). One difficulty with confluent drawing is that we haven't had good algorithms to tell which graphs can be drawn in this way, so instead we've had to rely on special cases that may only give a small subset of the confluently drawable graphs. But in the upward case, everything is much cleaner: it's possible to tell in polynomial time whether a transitively reduced DAG is upward confluent, and if so it's also possible to find a drawing that uses as few confluent junctions as possible. These results use some machinery from order theory: order dimension and the Dedekind–MacNeille completion. And as well as taking from order theory we give back to it with an efficient algorithm for completing two-dimensional partial orders. For instance, this technique can automatically turn a conventional drawing with crossings such as this:

A DAG whose upward drawing has quartically many crossings

into a confluent drawing such as this:

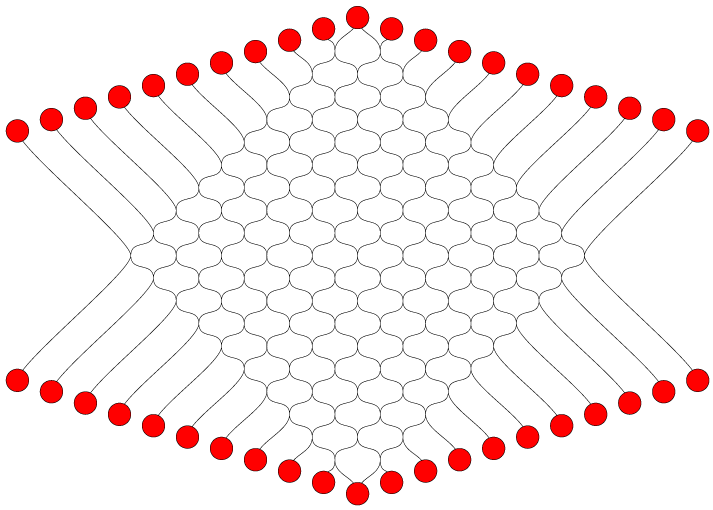
Confluent upward drawing of a DAG whose upward drawing has quartically many crossings

I think these are the first published research papers for UCI grad students Bannister and Simons, though Simons also has another one that just came out on retroactive range searching data structures, to appear at ISAAC.