By now you've probably seen the xkcd strip in which the alt text suggests the following game: start at a random Wikipedia article, and then repeatedly click the first link on the page until you get stuck or in a loop. With high probability, the page you ended up on was the one on Philosophy.

mat kelcey and Ilmari Karonen have crunched some numbers to show that it's actually true: some 94% of some 3 1/2 million Wikipedia articles eventually get into the same loop with Philosophy. The next largest components have around 20,000 articles, and after that it drops rapidly, with many components having double-digit sizes, many more having single digit sizes, and a huge number of two-article components.

My first thought when I saw these numbers was "Oh yes, the theory of random graphs predicts one giant component and a lot of tiny components". But then my second thought was, "Oh really? This is a very different kind of graph than the ones in that theory." It's a pseudoforest, a graph with exactly one outgoing link per node. Do random pseudoforests really behave like this?

To test the question, I wrote a program to generate random pseudoforests with approximately the same number of nodes (3 1/2 million), with each outgoing link chosen uniformly and independently at random from all the nodes. I ran it 200 times and made a scatterplot in which the horizontal axis is the size of the second-largest component (rather more informative than the largest, which is often near the size of the whole graph) and the vertical axis is the number of components. In my experiments the number of components ranged from 2 to 15 and the component size ranged from near zero to 1.7 million, nearly half the size of the whole graph.

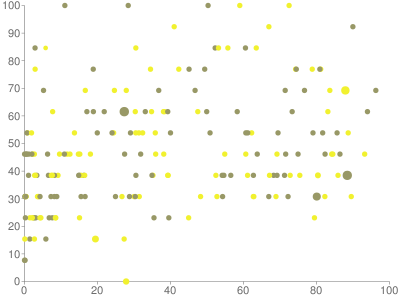
Second-largest component sizes of random pseudoforests versus number of components

To me, this looks not far from uniformly random, though with a bit of a positive correlation. The second largest component in Wikipedia would be at around the 1% mark on the horizontal axis, far to the left. To get a better picture of how it really fits into the data, I made a second plot with the same vertical scale but a logarithmic horizontal scale ranging from 2 to 6.5. On this scale, the Wikipedia second-largest-component size is around 52%, in the middle of the plot but not at all in the middle of the data.

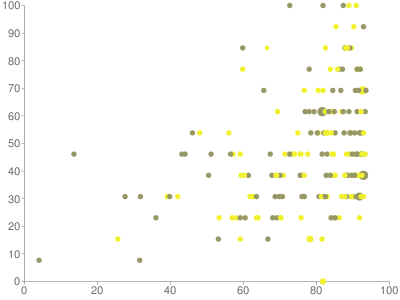
Second-largest component sizes of random pseudoforests, with a logarithmic horizontal scale

The reason Wikipedia isn't shown on these plots is because it's far off them. The horizontal coordinate (second largest component size) is within the plots, although far to the left of the median of the data, but the vertical coordinate (number of components) is enormous, far larger than the maximum of 15 that I saw with the random graphs.

To me, this shows convincingly that the pseudoforest generated from Wikipedia is very different from a random pseudoforest. It seems like an interesting problem to come up with a mathematical model that would fit it better.




Comments:

gareth_rees:

gareth_rees:
2011-08-24T15:41:50Z

I just tried this experimentally, starting at Special:Random, and I got the sequence:

Katre Türkay → Turkey → Eurasia → Continent → Landmass → Land → Earth → Planet → Astronomical object → Entity → Existence → Sense → Physiology → Science → Knowledge → Fact → Truth → Fact → ...

Is this the 20,000-article second-largest component? It seems quite big.

11011110:
2011-08-24T15:51:05Z
No, Fact has been edited since the xkcd comic came out (I think in large part to intentionally disrupt this game). It used to go Fact → Reality → Philosophy.
gareth_rees:
2011-08-24T15:52:33Z
Ah, I see from Ilmari Karonen's results that on the date the dump was taken (2011-05-26), the first link from [[Sense]] was to [[Perception]]. But the first link was quite volatile; in a couple of days around that date, the first link changed from [[Physiology]] to [[Organism]] to [[Perception]] and back to [[Physiology]].
the_harry_b: One note on the Wikipedia pseudoforest
2011-08-24T17:20:05Z

It seems to me that if you take a random set S of nodes in the Wikipedia pseudoforest, of size << N^1/2, then (if S is sufficiently large) with high probability the out-neighborhood of S will be smaller than S. This is because, due to Wikipedia's "in-house" style, a high proportion of articles begin "In [field of study]," or "[Subject] is a [nationality]..."

I don't know if this is enough to account for the statistics of the second-largest component, but it's a difference with an obvious explanation

11011110: Re: One note on the Wikipedia pseudoforest 2011-08-24T17:26:04Z Yes, I probably should have said, the length of the biggest cycle in Wikipedia is much smaller than the square root you would expect from a random pseudoforest. I think this may be closely related to what you are saying about sizes of out-neighborhoods.