Squaregraph sequences
I should probably post something about WADS but I haven't had time to get my thoughts in order yet. In the meantime here's something completely different. (For actual posts about WADS, see Kevin Wortman's brief post and John Moeller's cruise photos.)
Don Knuth has recently added six new integer sequences to OEIS involving biconnected squaregraphs, planar graphs in which all bounded faces are four-sided and in which all vertices are either on the unbounded face or are surrounded by four or more faces. Knuth wrote a program to enumerate biconnected squaregraphs and the OEIS sequences summarize its output.
As I described here, a squaregraph can be described by a chord diagram, a circular sequence of 2k symbols for some integer k, in which each of the symbols 1, 2, ..., k appears twice. Not all of the k!! possible chord diagrams work, though: a chord diagram corresponds to a squaregraph if it avoids the pattern i...j...k...i...j...k and the graph it describes is biconnected if it can't be decomposed into two smaller contiguous subsequences, with each symbol appearing in only one of the two subsequences.
For instance, as Knuth writes, there are (up to isomorphism) 18 biconnected squaregraphs with five bounded faces: the twelve pentominoes and six additional graphs.
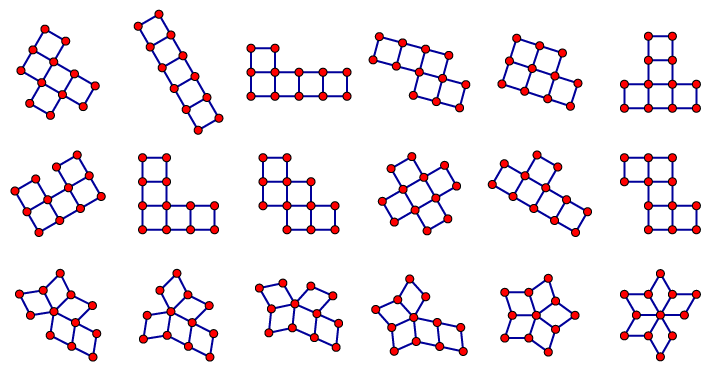
(Don't ask me why some of them came out tilted like that; it's an artifact of the implementation of my algorithm with Kevin for drawing squaregraphs with optimal angular resolution.)
The algorithms Knuth used to enumerate these things are pretty much just brute force searches, so there's probably plenty of room for more clever algorithms to push the sequences to greater numbers of terms.
Comments:
2011-08-19T00:55:26Z
I have even found a way to compile it:
http://ideone.com/aLghS
It needs unittests and more.