Something I started doing over at Google+ that seems to have been well received there was to share links to new or newly-expanded Wikipedia articles (primarily the ones I'd worked on) about technical topics related to algorithms and combinatorics. I don't see a reason to stop doing that now that my G+ account is on hiatus, so anyway, here's another one, inspired by a recent question on the TCS Exchange:

Well-covered graph. These are the graphs in which all maximal independent sets have the same size, so (if you know a graph is well-covered) you can easily find a maximum independent set. Unfortunately, it's hard to tell whether an unknown graph is well-covered...

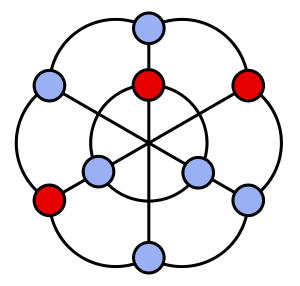
A well-covered graph, the intersection graph of the nine diagonals of a hexagon

The graph in the image may be used to represent triangulations of the hexagon: the three inner vertices of the graph represent the three long diagonals of the hexagon, the six outer vertices represent the six short diagonals, and an independent set represents the set of diagonals in a triangulation. Since every triangulation of the hexagon has the same number of edges, every independent set in the graph has the same number of vertices. The same graph also turns out to be a member of the Petersen family, conveniently for me as I could grab and edit an image I'd already drawn instead of having to do it again from scratch.




Comments:

ext_274121:
2011-08-11T00:04:32Z

It might be interesting to explore which "hard" graph problems remain hard on inputs which come from some easily-recognizable subset of well-covered graphs.

For example, for the Lexicographically First Maximal Independent Set problem, which is P-complete on general graphs, I believe the reduction (from the Circuit Value problem) could be modified to show the same for a class of graphs which are clearly well-covered. (I haven't checked the details, though.)

-Andy D.

11011110:
2011-08-11T00:15:10Z

There's something of that flavor in one of the papers I didn't include in the Wikipedia article (I was trying to be selective rather than just summarizing all of the ~100 papers on the subject):

Sankaranarayana, Ramesh S. Tracking the P-NP boundary for well-covered graphs. Networks 29 (1997), no. 1, 29–37. MR1423743.

They look at four classes of graphs (well covered, very well covered, and two less natural classes in between) and show that they can be distinguished from each other by which of several problems are hard or easy on which classes.

As for LFMIS, I think the reduction from the general problem to the well-covered case by adding a degree-one neighbor to each vertex and putting those new neighbors last in the lexicographic ordering should work. But maybe it's just as easy to modify the original reduction as you say.